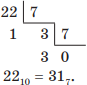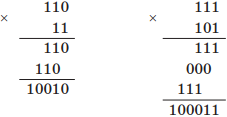Информация и ее кодирование
Различные подходы к определению понятия «информация». Виды информационных
процессов. Информационный аспект в деятельности человека
Информация (лат. informatio — разъяснение, изложение, набор сведений) — базовое понятие в информатике, которому нельзя дать строгого определения, а можно только пояснить:
- информация — это новые факты, новые знания;
- информация — это сведения об объектах и явлениях окружающей среды, которые повышают уровень осведомленности человека;
- информация — это сведения об объектах и явлениях окружающей среды, которые уменьшают степень неопределенности знаний об этих объектах или явлениях при принятии определенных решений.
Понятие «информация» является общенаучным, т. е. используется в различных науках: физике, биологии, кибернетике, информатике и др. При этом в каждой науке данное понятие связано с различными системами понятий. Так, в физике информация рассматривается как антиэнтропия (мера упорядоченности и сложности системы). В биологии понятие «информация» связывается с целесообразным поведением живых организмов, а также с исследованиями механизмов наследственности. В кибернетике понятие «информация» связано с процессами управления в сложных системах.
Основными социально значимыми свойствами информации являются:
- полезность;
- доступность (понятность);
- актуальность;
- полнота;
- достоверность;
- адекватность.
В человеческом обществе непрерывно протекают информационные процессы: люди воспринимают информацию из окружающего мира с помощью органов чувств, осмысливают ее и принимают определенные решения, которые, воплощаясь в реальные действия, воздействуют на окружающий мир.
Информационный процесс — это процесс сбора (приема), передачи (обмена), хранения, обработки (преобразования) информации.
Сбор информации — это процесс поиска и отбора необходимых сообщений из разных источников (работа со специальной литературой, справочниками; проведение экспериментов; наблюдения; опрос, анкетирование; поиск в информационно-справочных сетях и системах и т. д.).
Передача информации — это процесс перемещения сообщений от источника к приемнику по каналу передачи. Информация передается в форме сигналов — звуковых, световых, ультразвуковых, электрических, текстовых, графических и др. Каналами передачи могут быть воздушное пространство, электрические и оптоволоконные кабели, отдельные люди, нервные клетки человека и т. д.
Хранение информации — это процесс фиксирования сообщений на материальном носителе. Сейчас для хранения информации используются бумага, деревянные, тканевые, металлические и другие поверхности, кино- и фотопленки, магнитные ленты, магнитные и лазерные диски, флэш-карты и др.
Обработка информации — это процесс получения новых сообщений из имеющихся. Обработка информации является одним из основных способов увеличения ее количества. В результате обработки из сообщения одного вида можно получить сообщения других видов.
Защита информации — это процесс создания условий, которые не допускают случайной потери, повреждения, изменения информации или несанкционированного доступа к ней. Способами защиты информации являются создание ее резервных копий, хранение в защищенном помещении, предоставление пользователям соответствующих прав доступа к информации, шифрование сообщений и др.
Язык как способ представления и передачи информации
Для того чтобы сохранить информацию и передать ее, с давних времен использовались знаки.
В зависимости от способа восприятия знаки делятся на:
- зрительные (буквы и цифры, математические знаки, музыкальные ноты, дорожные знаки и др.);
- слуховые (устная речь, звонки, сирены, гудки и др.);
- осязательные (азбука Брайля для слепых, жесты-касания и др.);
- обонятельные;
- вкусовые.
Для долговременного хранения знаки записывают на носители информации.
Для передачи информации используются знаки в виде сигналов (световые сигналы светофора, звуковой сигнал школьного звонка и т. д.).
По способу связи между формой и значением знаки делятся на:
- иконические — их форма похожа на отображаемый объект (например, значок папки «Мой компьютер» на «Рабочем столе» компьютера);
- символы — связь между их формой и значением устанавливается по общепринятому соглашению (например, буквы, математические символы ∫, ≤, ⊆, ∞; символы химических элементов).
Для представления информации используются знаковые системы, которые называются языками. Основу любого языка составляет алфавит — набор символов, из которых формируется сообщение, и набор правил выполнения операций над символами.
Языки делятся на:
- естественные (разговорные) — русский, английский, немецкий и др.;
- формальные — встречающиеся в специальных областях человеческой деятельности (например, язык алгебры, языки программирования, электрических схем и др.)
Системы счисления также можно рассматривать как формальные языки. Так, десятичная система счисления — это язык, алфавит которого состоит из десяти цифр 0..9, двоичная система счисления — язык, алфавит которого состоит из двух цифр — 0 и 1.
Методы измерения количества информации: вероятностный и алфавитный
Единицей измерения количества информации является бит. 1 бит — это количество информации, содержащейся в сообщении, которое вдвое уменьшает неопределенность знаний о чем-либо.
Связь между количеством возможных событий N и количеством информации I определяется формулой Хартли:
N = 2I.
Например, пусть шарик находится в одной из четырех коробок. Таким образом, имеется четыре равновероятных события (N = 4). Тогда по формуле Хартли 4 = 2I. Отсюда I = 2. То есть сообщение о том, в какой именно коробке находится шарик, содержит 2 бита информации.
Алфавитный подход
При алфавитном подходе к определению количества информации отвлекаются от содержания (смысла) информации и рассматривают ее как последовательность знаков определенной знаковой системы. Набор символов языка (алфавит) можно рассматривать как различные возможные события. Тогда, если считать, что появление символов в сообщении равновероятно, по формуле Хартли можно рассчитать, какое количество информации несет каждый символ:
I = log2 N.
Например, в русском языке 32 буквы (буква ё обычно не используется), т. е. количество событий будет равно 32. Тогда информационный объем одного символа будет равен:
I = log2 32 = 5 битов.
Если N не является целой степенью 2, то число log2N не является целым числом, и для I надо выполнять округление в большую сторону. При решении задач в таком случае I можно найти как log2N’, где N′ — ближайшая к N степень двойки — такая, что N′ > N.
Например, в английском языке 26 букв. Информационный объем одного символа можно найти так:
N = 26; N’ = 32; I = log2N’ = log2(25) = 5 битов.
Если количество символов алфавита равно N, а количество символов в записи сообщения равно М, то информационный объем данного сообщения вычисляется по формуле:
I = M · log2N.
Примеры решения задач
Пример 1. Световое табло состоит из лампочек, каждая из которых может находиться в одном из двух состояний («включено» или «выключено»). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 50 различных сигналов?
Решение. С помощью n лампочек, каждая из которых может находиться в одном из двух состояний, можно закодировать 2n сигналов. 25 < 50 < 26, поэтому пяти лампочек недостаточно, а шести хватит.
Ответ: 6.
Пример 2. Метеорологическая станция ведет наблюдения за влажностью воздуха. Результатом одного измерения является целое число от 0 до 100, которое записывается при помощи минимально возможного количества битов. Станция сделала 80 измерений. Определите информационный объем результатов наблюдений.
Решение. В данном случае алфавитом является множество целых чисел от 0 до 100. Всего таких значений 101. Поэтому информационный объем результатов одного измерения I = log2101. Это значение не будет целочисленным. Заменим число 101 ближайшей к нему степенью двойки, большей 101. Это число 128 = 27. Принимаем для одного измерения I = log2128 = 7 битов. Для 80 измерений общий информационный объем равен:
80 · 7 = 560 битов = 70 байтов.
Ответ: 70 байтов.
Вероятностный подход
Вероятностный подход к измерению количества информации применяют, когда возможные события имеют различные вероятности реализации. В этом случае количество информации определяют по формуле Шеннона:
$I=-∑↙{i=1}↖{N}p_ilog_2p_i$,
где $I$ — количество информации;
$N$ — количество возможных событий;
$p_i$ — вероятность $i$-го события.
Например, пусть при бросании несимметричной четырехгранной пирамидки вероятности отдельных событий будут равны:
$p_1={1}/{2}, p_2={1}/{4}, p_3={1}/{8}, p_4={1}/{8}$.
Тогда количество информации, которое будет получено после реализации одного из них, можно вычислить по формуле Шеннона:
$I=-({1}/{2}·log_2{1}/{2}+{1}/{4}·log_2{1}/{4}+{1}/{8}·log_2{1}/{8}+{1}/{8}·log_2{1}/{8})={14}/{8}$ битов $= 1.75 $бита.
Единицы измерения количества информации
Наименьшей единицей информации является бит (англ. binary digit (bit) — двоичная единица информации).
Бит — это количество информации, необходимое для однозначного определения одного из двух равновероятных событий. Например, один бит информации получает человек, когда он узнает, опаздывает с прибытием нужный ему поезд или нет, был ночью мороз или нет, присутствует на лекции студент Иванов или нет и т. д.
В информатике принято рассматривать последовательности длиной 8 битов. Такая последовательность называется байтом.
Производные единицы измерения количества информации:
1 байт = 8 битов
1 килобайт (Кб) = 1024 байта = 210 байтов
1 мегабайт (Мб) = 1024 килобайта = 220 байтов
1 гигабайт (Гб) = 1024 мегабайта = 230 байтов
1 терабайт (Тб) = 1024 гигабайта = 240 байтов
Процесс передачи информации. Виды и свойства источников и приемников информации. Сигнал, кодирование и декодирование, причины искажения информации при передаче
Информация передается в виде сообщений от некоторого источника информации к ее приемнику посредством канала связи между ними.
В качестве источника информации может выступать живое существо или техническое устройство. Источник посылает передаваемое сообщение, которое кодируется в передаваемый сигнал.
Сигнал — это материально-энергетическая форма представления информации. Другими словами, сигнал — это переносчик информации, один или несколько параметров которого, изменяясь, отображают сообщение. Сигналы могут быть аналоговыми (непрерывными) или дискретными (импульсными).
Сигнал посылается по каналу связи. В результате в приемнике появляется принимаемый сигнал, который декодируется и становится принимаемым сообщением.
Передача информации по каналам связи часто сопровождается воздействием помех, вызывающих искажение и потерю информации.
Примеры решения задач
Пример 1. Для кодирования букв А, З, Р, О используются двухразрядные двоичные числа 00, 01, 10, 11 соответственно. Этим способом закодировали слово РОЗА и результат записали шестнадцатеричным кодом. Указать полученное число.
Решение. Запишем последовательность кодов для каждого символа слова РОЗА: 10 11 01 00. Если рассматривать полученную последовательность как двоичное число, то в шестнадцатеричном коде оно будет равно: 1011 01002 = В416.
Ответ: В416.
Скорость передачи информации и пропускная способность канала связи
Прием/передача информации может происходить с разной скоростью. Количество информации, передаваемое за единицу времени, есть скорость передачи информации, или скорость информационного потока.
Скорость выражается в битах в секунду (бит/с) и кратных им Кбит/с и Мбит/с, а также в байтах в секунду (байт/с) и кратных им Кбайт/с и Мбайт/с.
Максимальная скорость передачи информации по каналу связи называется пропускной способностью канала.
Примеры решения задач
Пример 1. Скорость передачи данных через ADSL-соединение равна 256000 бит/с. Передача файла через данное соединение заняла 3 мин. Определите размер файла в килобайтах.
Решение. Размер файла можно вычислить, если умножить скорость передачи информации на время передачи. Выразим время в секундах: 3 мин = 3 ⋅ 60 = 180 с. Выразим скорость в килобайтах в секунду: 256000 бит/с = 256000 : 8 : 1024 Кбайт/с. При вычислении размера файла для упрощения расчетов выделим степени двойки:
Размер файла = (256000 : 8 : 1024) ⋅ (3 ⋅ 60) = (28 ⋅ 103 : 23 : 210) ⋅ (3 ⋅ 15 ⋅ 22) = (28 ⋅ 125 ⋅ 23 : 23 : 210) ⋅ (3 ⋅ 15 ⋅ 22) = 125 ⋅ 45 = 5625 Кбайт.
Ответ: 5625 Кбайт.
Представление числовой информации. Сложение и умножение в разных системах счисления
Представление числовой информации с помощью систем счисления
Для представления информации в компьютере используется двоичный код, алфавит которого состоит из двух цифр — 0 и 1. Каждая цифра машинного двоичного кода несет количество информации, равное одному биту.
Система счисления — это система записи чисел с помощью определенного набора цифр.
Система счисления называется позиционной, если одна и та же цифра имеет различное значение, которое определяется ее местом в числе.
Позиционной является десятичная система счисления. Например, в числе 999 цифра «9» в зависимости от позиции означает 9, 90, 900.
Римская система счисления является непозиционной. Например, значение цифры Х в числе ХХІ остается неизменным при вариации ее положения в числе.
Позиция цифры в числе называется разрядом. Разряд числа возрастает справа налево, от младших разрядов к старшим.
Количество различных цифр, употребляемых в позиционной системе счисления, называется ее основанием.
Развернутая форма числа — это запись, которая представляет собой сумму произведений цифр числа на значение позиций.
Например: 8527 = 8 ⋅ 103 + 5 ⋅ 102 + 2 ⋅ 101 + 7 ⋅ 100.
Развернутая форма записи чисел произвольной системы счисления имеет вид
$∑↙{i=n-1}↖{-m}a_iq^i$,
где $X$ — число;
$a$ — цифры численной записи, соответствующие разрядам;
$i$ — индекс;
$m$ — количество разрядов числа дробной части;
$n$ — количество разрядов числа целой части;
$q$ — основание системы счисления.
Например, запишем развернутую форму десятичного числа $327.46$:
$n=3, m=2, q=10.$
$X=∑↙{i=2}↖{-2}a_iq^i=a_2·10^2+a_1·10^1+a_0·10^0+a_{-1}·10^{-1}+a_{-2}·10^{-2}=3·10^2+2·10^1+7·10^0+4·10^{-1}+6·10^{-2}$
Если основание используемой системы счисления больше десяти, то для цифр вводят условное обозначение со скобкой вверху или буквенное обозначение: В — двоичная система, О — восмеричная, Н — шестнадцатиричная.
Например, если в двенадцатеричной системе счисления 10 = А, а 11 = В, то число 7А,5В12 можно расписать так:
7А,5В12 = В ⋅ 12-2 + 5 ⋅ 2-1 + А ⋅ 120 + 7 ⋅ 121.
В шестнадцатеричной системе счисления 16 цифр, обозначаемых 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, что соответствует следующим числам десятеричной системы счисления: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15. Примеры чисел: 17D,ECH; F12AH.
Перевод чисел в позиционных системах счисления
Перевод чисел из произвольной системы счисления в десятичную
Для перевода числа из любой позиционной системы счисления в десятичную необходимо использовать развернутую форму числа, заменяя, если это необходимо, буквенные обозначения соответствующими цифрами. Например:
11012 = 1 ⋅ 23 + 1 ⋅ 22 + 0 ⋅ 21 + 1 ⋅ 20 = 1310;
17D,ECH = 12 ⋅ 16–2 + 14 ⋅ 16–1 + 13 ⋅ 160 + 7 ⋅ 161 + 1 ⋅ 162 = 381,921875.
Перевод чисел из десятичной системы счисления в заданную
Для преобразования целого числа десятичной системы счисления в число любой другой системы счисления последовательно выполняют деление нацело на основание системы счисления, пока не получат нуль. Числа, которые возникают как остаток от деления на основание системы, представляют собой последовательную запись разрядов числа в выбранной системе счисления от младшего разряда к старшему. Поэтому для записи самого числа остатки от деления записывают в обратном порядке.
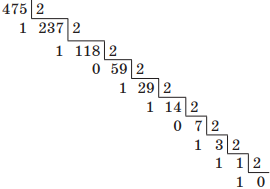
Например, переведем десятичное число 475 в двоичную систему счисления. Для этого будем последовательно выполнять деление нацело на основание новой системы счисления, т. е. на 2:
Читая остатки от деления снизу вверх, получим 111011011.
Проверка:
1 ⋅ 28 + 1 ⋅ 27 + 1 ⋅ 26 + 0 ⋅ 25 + 1 ⋅ 24 + 1 ⋅ 23 + 0 ⋅ 22 + 1 ⋅ 21 + 1 ⋅ 20 = 1 + 2 + 8 + 16 + 64 + 128 + 256 = 47510.
Для преобразования десятичных дробей в число любой системы счисления последовательно выполняют умножение на основание системы счисления, пока дробная часть произведения не будет равна нулю. Полученные целые части являются разрядами числа в новой системе, и их необходимо представлять цифрами этой новой системы счисления. Целые части в дальнейшем отбрасываются.
Например, переведем десятичную дробь 0,37510 в двоичную систему счисления:
Полученный результат — 0,0112.
Не каждое число может быть точно выражено в новой системе счисления, поэтому иногда вычисляют только требуемое количество разрядов дробной части.
Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную и обратно
Для записи восьмеричных чисел используются восемь цифр, т. е. в каждом разряде числа возможны 8 вариантов записи. Каждый разряд восьмеричного числа содержит 3 бита информации (8 = 2І; І = 3).
Таким образом, чтобы из восьмеричной системы счисления перевести число в двоичный код, необходимо каждую цифру этого числа представить триадой двоичных символов. Лишние нули в старших разрядах отбрасываются.
Например:
1234,7778 = 001 010 011 100,111 111 1112 = 1 010 011 100,111 111 1112;
12345678 = 001 010 011 100 101 110 1112 = 1 010 011 100 101 110 1112.
При переводе двоичного числа в восьмеричную систему счисления нужно каждую триаду двоичных цифр заменить восьмеричной цифрой. При этом, если необходимо, число выравнивается путем дописывания нулей перед целой частью или после дробной.
Например:
11001112 = 001 100 1112 = 1478;
11,10012 = 011,100 1002 = 3,448;
110,01112 = 110,011 1002 = 6,348.
Для записи шестнадцатеричных чисел используются шестнадцать цифр, т. е. для каждого разряда числа возможны 16 вариантов записи. Каждый разряд шестнадцатеричного числа содержит 4 бита информации (16 = 2І; І = 4).
Таким образом, для перевода двоичного числа в шестнадцатеричное его нужно разбить на группы по четыре цифры и преобразовать каждую группу в шестнадцатеричную цифру.
Например:
11001112 = 0110 01112 = 6716;
11,10012 = 0011,10012 = 3,916;
110,01110012 = 0110,0111 00102 = 65,7216.
Для перевода шестнадцатеричного числа в двоичный код необходимо каждую цифру этого числа представить четверкой двоичных цифр.
Например:
1234,AB7716 = 0001 0010 0011 0100,1010 1011 0111 01112 = 1 0010 0011 0100,1010 1011 0111 01112;
CE456716 = 1100 1110 0100 0101 0110 01112.
При переводе числа из одной произвольной системы счисления в другую нужно выполнить промежуточное преобразование в десятичное число. При переходе из восьмеричного счисления в шестнадцатеричное и обратно используется вспомогательный двоичный код числа.
Например, переведем троичное число 2113 в семеричную систему счисления. Для этого сначала преобразуем число 2113 в десятичное, записав его развернутую форму:
2113 = 2 ⋅ 32 + 1 ⋅ 31 + 1 ⋅ 30 = 18 + 3 + 1 = 2210.
Затем переведем десятичное число 2210 в семеричную систему счисления делением нацело на основание новой системы счисления, т. е. на 7:
Итак, 2113 = 317.
Примеры решения задач
Пример 1. В системе счисления с некоторым основанием число 12 записывается в виде 110. Указать это основание.
Решение. Обозначим искомое основание п. По правилу записи чисел в позиционных системах счисления 1210 = 110n = 0 ·n0 + 1 · n1 + 1 · n2. Составим уравнение: n2 + n = 12 . Найдем натуральный корень уравнения (отрицательный корень не подходит, т. к. основание системы счисления, по определению, натуральное число большее единицы): n = 3 . Проверим полученный ответ: 1103 = 0· 30 + 1 · 31 + 1 · 32 = 0 + 3 + 9 = 12 .
Ответ: 3.
Пример 2. Указать через запятую в порядке возрастания все основания систем счисления, в которых запись числа 22 оканчивается на 4.
Решение. Последняя цифра в записи числа представляет собой остаток от деления числа на основание системы счисления. 22 — 4 = 18. Найдем делители числа 18. Это числа 2, 3, 6, 9, 18. Числа 2 и 3 не подходят, т. к. в системах счисления с основаниями 2 и 3 нет цифры 4. Значит, искомыми основаниями являются числа 6, 9 и 18. Проверим полученный результат, записав число 22 в указанных системах счисления: 2210 = 346 = 249 = 1418.
Ответ: 6, 9, 18.
Пример 3. Указать через запятую в порядке возрастания все числа, не превосходящие 25, запись которых в двоичной системе счисления оканчивается на 101. Ответ записать в десятичной системе счисления.
Решение. Для удобства воспользуемся восьмеричной системой счисления. 1012 = 58. Тогда число х можно представить как x = 5 · 80 + a1 · 81 + a2 · 82 + a3 · 83 + … , где a1, a2, a3, … — цифры восьмеричной системы. Искомые числа не должны превосходить 25, поэтому разложение нужно ограничить двумя первыми слагаемыми ( 82 > 25), т. е. такие числа должны иметь представление x = 5 + a1 · 8. Поскольку x ≤ 25 , допустимыми значениями a1 будут 0, 1, 2. Подставив эти значения в выражение для х, получим искомые числа:
a1 = 0; x = 5 + 0 · 8 = 5;.
a1=1; x = 5 + 1 · 8 = 13;.
a1 = 2; x = 5 + 2 · 8 = 21;.
Выполним проверку:
510 = 1012;
1310 = 11012;
2110 = 101012.
Ответ: 5, 13, 21.
Арифметические операции в позиционных системах счисления
Правила выполнения арифметических действий над двоичными числами задаются таблицами сложения, вычитания и умножения.
| Сложение | Вычитание | Умножение |
| 0 + 0 = 0 | 0 – 0 = 0 | 0 ⋅ 0 = 0 |
| 0 + 1 = 1 | 1 – 0 = 1 | 0 ⋅ 1 = 0 |
| 1 + 0 = 1 | 1 – 1 = 0 | 1 ⋅ 0 = 0 |
| 1 + 1 = 10 | 10 – 1 = 1 | 1 ⋅ 1 = 1 |
Правило выполнения операции сложения одинаково для всех систем счисления: если сумма складываемых цифр больше или равна основанию системы счисления, то единица переносится в следующий слева разряд. При вычитании, если необходимо, делают заем.
Пример выполнения сложения: сложим двоичные числа 111 и 101, 10101 и 1111:
Пример выполнения вычитания: вычтем двоичные числа 10001 – 101 и 11011 – 1101:
Пример выполнения умножения: умножим двоичные числа 110 и 11, 111 и 101:
Аналогично выполняются арифметические действия в восьмеричной, шестнадцатеричной и других системах счисления. При этом необходимо учитывать, что величина переноса в следующий разряд при сложении и заем из старшего разряда при вычитании определяется величиной основания системы счисления.
Например, выполним сложение восьмеричных чисел 368 и 158, а также вычитание шестнадцатеричных чисел 9С16 и 6716:
При выполнении арифметических операций над числами, представленными в разных системах счисления, нужно предварительно перевести их в одну и ту же систему.
Представление чисел в компьютере
Формат с фиксированной запятой
В памяти компьютера целые числа хранятся в формате с фиксированной запятой: каждому разряду ячейки памяти соответствует один и тот же разряд числа, «запятая» находится вне разрядной сетки.
Для хранения целых неотрицательных чисел отводится 8 битов памяти. Минимальное число соответствует восьми нулям, хранящимся в восьми битах ячейки памяти, и равно 0. Максимальное число соответствует восьми единицам и равно
1 ⋅ 27 + 1 ⋅ 26 + 1 ⋅ 25 + 1 ⋅ 24 + 1 ⋅ 23 + 1 ⋅ 22 + 1 ⋅ 21 + 1 ⋅ 20 = 25510.
Таким образом, диапазон изменения целых неотрицательных чисел — от 0 до 255.
Для п-разрядного представления диапазон будет составлять от 0 до 2n – 1.
Для хранения целых чисел со знаком отводится 2 байта памяти (16 битов). Старший разряд отводится под знак числа: если число положительное, то в знаковый разряд записывается 0, если число отрицательное — 1. Такое представление чисел в компьютере называется прямым кодом.
Для представления отрицательных чисел используется дополнительный код. Он позволяет заменить арифметическую операцию вычитания операцией сложения, что существенно упрощает работу процессора и увеличивает его быстродействие. Дополнительный код отрицательного числа А, хранящегося в п ячейках, равен 2n − |А|.
Алгоритм получения дополнительного кода отрицательного числа:
1. Записать прямой код числа в п двоичных разрядах.
2. Получить обратный код числа. (Обратный код образуется из прямого кода заменой нулей единицами, а единиц — нулями, кроме цифр знакового разряда. Для положительных чисел обратный код совпадает с прямым. Используется как промежуточное звено для получения дополнительного кода.)
3. Прибавить единицу к полученному обратному коду.
Например, получим дополнительный код числа –201410 для шестнадцатиразрядного представления:
| Прямой код | Двоичный код числа 201410 со знаковым разрядом | 1000011111011110 |
| Обратный код | Инвертирование (исключая знаковый разряд) | 1111100000100001 |
| Прибавление единицы | 1111100000100001 + 0000000000000001 | |
| Дополнительный код | 1111100000100010 |
При алгебраическом сложении двоичных чисел с использованием дополнительного кода положительные слагаемые представляют в прямом коде, а отрицательные — в дополнительном коде. Затем суммируют эти коды, включая знаковые разряды, которые при этом рассматриваются как старшие разряды. При переносе из знакового разряда единицу переноса отбрасывают. В результате получают алгебраическую сумму в прямом коде, если эта сумма положительная, и в дополнительном — если сумма отрицательная.
Например:
1) Найдем разность 1310 – 1210 для восьмибитного представления. Представим заданные числа в двоичной системе счисления:
1310 = 11012 и 1210 = 11002.
Запишем прямой, обратный и дополнительный коды для числа –1210 и прямой код для числа 1310 в восьми битах:
| 1310 | –1210 | |
| Прямой код | 00001101 | 10001100 |
| Обратный код | — | 11110011 |
| Дополнительный код | — | 11110100 |
Вычитание заменим сложением (для удобства контроля за знаковым разрядом условно отделим его знаком «_»):
Так как произошел перенос из знакового разряда, первую единицу отбрасываем, и в результате получаем 00000001.
2) Найдем разность 810 – 1310 для восьмибитного представления.
Запишем прямой, обратный и дополнительный коды для числа –1310 и прямой код для числа 810 в восьми битах:
| 810 | –1310 | |
| Прямой код | 00001000 | 10001101 |
| Обратный код | — | 11110010 |
| Дополнительный код | — | 11110011 |
Вычитание заменим сложением:
В знаковом разряде стоит единица, а значит, результат получен в дополнительном коде. Перейдем от дополнительного кода к обратному, вычтя единицу:
11111011 – 00000001 = 11111010.
Перейдем от обратного кода к прямому, инвертируя все цифры, за исключением знакового (старшего) разряда: 10000101. Это десятичное число –510.
Так как при п-разрядном представлении отрицательного числа А в дополнительном коде старший разряд выделяется для хранения знака числа, минимальное отрицательное число равно: А = –2n–1, а максимальное: |А| = 2n–1 или А = –2n–1 – 1.
Определим диапазон чисел, которые могут храниться в оперативной памяти в формате длинных целых чисел со знаком (для хранения таких чисел отводится 32 бита памяти). Минимальное отрицательное число равно
А = –231 = –214748364810.
Максимальное положительное число равно
А = 231 – 1 = 214748364710.
Достоинствами формата с фиксированной запятой являются простота и наглядность представления чисел, простота алгоритмов реализации арифметических операций. Недостатком является небольшой диапазон представимых чисел, недостаточный для решения большинства прикладных задач.
Формат с плавающей запятой
Вещественные числа хранятся и обрабатываются в компьютере в формате с плавающей запятой, использующем экспоненциальную форму записи чисел.
Число в экспоненциальном формате представляется в таком виде:
$A=m·q^n$,
где $m$ — мантисса числа (правильная отличная от нуля дробь);
$q$ — основание системы счисления;
$n$ — порядок числа.
Например, десятичное число 2674,381 в экспоненциальной форме запишется так:
2674,381 = 0,2674381 ⋅ 104.
Число в формате с плавающей запятой может занимать в памяти 4 байта (обычная точность) или 8 байтов (двойная точность). При записи числа выделяются разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы. Две последние величины определяют диапазон изменения чисел и их точность.
Определим диапазон (порядок) и точность (мантиссу) для формата чисел обычной точности, т. е. четырехбайтных. Из 32 битов 8 выделяется для хранения порядка и его знака и 24 — для хранения мантиссы и ее знака.
Найдем максимальное значение порядка числа. Из 8 разрядов старший разряд используется для хранения знака порядка, остальные 7 — для записи величины порядка. Значит, максимальное значение равно 11111112 = 12710. Так как числа представляются в двоичной системе счисления, то
$q^n = 2^{127}≈ 1.7 · 10^{38}$.
Аналогично, максимальное значение мантиссы равно
$m = 2^{23} — 1 ≈ 2^{23} = 2^{(10 · 2.3)} ≈ 1000^{2.3} = 10^{(3 · 2.3)} ≈ 10^7$.
Таким образом, диапазон чисел обычной точности составляет $±1.7 · 10^{38}$.
Кодирование текстовой информации. Кодировка ASCII. Основные используемые кодировки кириллицы
Соответствие между набором символов и набором числовых значений называется кодировкой символа. При вводе в компьютер текстовой информации происходит ее двоичное кодирование. Код символа хранится в оперативной памяти компьютера. В процессе вывода символа на экран производится обратная операция — декодирование, т. е. преобразование кода символа в его изображение.
Присвоенный каждому символу конкретный числовой код фиксируется в кодовых таблицах. Одному и тому же символу в разных кодовых таблицах могут соответствовать разные числовые коды. Необходимые перекодировки текста обычно выполняют специальные программы-конверторы, встроенные в большинство приложений.
Как правило, для хранения кода символа используется один байт (восемь битов), поэтому коды символов могут принимать значение от 0 до 255. Такие кодировки называют однобайтными. Они позволяют использовать 256 символов ( N = 2I = 28 = 256 ). Таблица однобайтных кодов символов называется ASCII (American Standard Code for Information Interchange — Американский стандартный код для обмена информацией). Первая часть таблицы ASCII-кодов (от 0 до 127) одинакова для всех IBM-PC совместимых компьютеров и содержит:
- коды управляющих символов;
- коды цифр, арифметических операций, знаков препинания;
- некоторые специальные символы;
- коды больших и маленьких латинских букв.
Вторая часть таблицы (коды от 128 до 255) бывает различной в различных компьютерах. Она содержит коды букв национального алфавита, коды некоторых математических символов, коды символов псевдографики. Для русских букв в настоящее время используется пять различных кодовых таблиц: КОИ-8, СР1251, СР866, Мас, ISO.
В последнее время широкое распространение получил новый международный стандарт Unicode. В нем отводится по два байта (16 битов) для кодирования каждого символа, поэтому с его помощью можно закодировать 65536 различных символов ( N = 216 = 65536 ). Коды символов могут принимать значение от 0 до 65535.
Примеры решения задач
Пример. С помощью кодировки Unicode закодирована следующая фраза:
Я хочу поступить в университет!
Оценить информационный объем этой фразы.
Решение. В данной фразе содержится 31 символ (включая пробелы и знак препинания). Поскольку в кодировке Unicode каждому символу отводится 2 байта памяти, для всей фразы понадобится 31 ⋅ 2 = 62 байта или 31 ⋅ 2 ⋅ 8 = 496 битов.
Ответ: 32 байта или 496 битов.
Мы ежедневно работаем с информацией из разных источников. При этом каждый из нас имеет некоторые интуитивные представления о том, что означает, что один источник является для нас более информативным, чем другой. Однако далеко не всегда понятно, как это правильно определить формально. Не всегда большое количество текста означает большое количество информации. Например, среди СМИ распространена практика, когда короткое сообщение из ленты информационного агентства переписывают в большую новость, но при этом не добавляют никакой «новой информации». Или другой пример: рассмотрим текстовый файл с романом Л.Н. Толстого «Война и мир» в кодировке UTF-8. Его размер — 3.2 Мб. Сколько информации содержится в этом файле? Изменится ли это количество, если файл перекодировать в другую кодировку? А если заархивировать? Сколько информации вы получите, если прочитаете этот файл? А если прочитаете его второй раз?
По мотивам открытой лекции для Computer Science центра рассказываю о том, как можно математически подойти к определению понятия «количество информации».
В классической статье А.Н. Колмогорова «Три подхода к определению понятия количества информации» (1965) рассматривают три способа это сделать:
-
комбинаторный (информация по Хартли),
-
вероятностный (энтропия Шеннона),
-
алгоритмический (колмогоровская сложность).
Мы будем следовать этому плану.
Комбинаторный подход: информация по Хартли
Мы начнём самого простого и естественного подхода, предложенного Хартли в 1928 году.
Пусть задано некоторое конечное множество . Количеством информации в
будем называть
.
Можно интерпретировать это определение следующим образом: нам нужно битов для описания элемента из
.
Почему мы используем биты? Можно использовать и другие единицы измерения, например, триты или байты, но тогда нужно изменить основание логарифма на 3 или 256, соответственно. В дальшейшем все логарифмы будут по основанию 2.
Этого определения уже достаточно для того, чтобы измерить количество информации в некотором сообщении. Пусть про стало известно, что
. Теперь нам достаточно
битов для описания
, таким образом нам сообщили
битов информации.
Пример
Загадано целое число
от
до
. Нам сообщили, что
делится на
. Сколько информации нам сообщили?
Воспользуемся рассуждением выше.
(Тот факт, что некоторое сообщение может содержать нецелое количество битов, может показаться немного неожиданным.)
Можно ещё сказать, что сообщение, уменшающее пространство поиска в раз приносит
битов информации. В данном примере пространство поиска уменьшилось в 1000/166 раз.
Интересно, что одного этого определения уже достаточно для того, чтобы решать довольно нетривиальные задачи.
Применение: цена информации
Загадано целое число
от
до
. Разрешается задавать любые вопросы на ДА/НЕТ. Если ответ на вопрос «ДА», то мы должны заплатить рубль, если ответ «НЕТ» — два рубля. Сколько нужно заплатить для отгадывания числа
?
Любой вопрос можно сформулировать как вопрос о принадлежности некоторому множеству, поэтому мы будем считать, что все вопросы имеют вид «?» для некоторого множества
.
Каким образом нужно задавать вопросы? Нам бы хотелось, чтобы вне зависимости от ответа цена за бит информации была постоянной. Другими словами, в случае ответа «НЕТ» и заплатив два рубля мы должны узнать в два больше информации, чем при ответе «ДА». Давайте запишем это формально.
Потребуем, чтобы
Пусть , тогда
. Подставляем и получаем, что
Это эквивалентно квадратному уравнению Положительный корень этого уравнения
. Таким образом, при любом ответе мы заплатим
рублей за бит информации, а в сумме мы заплатим примерно
рублей (с точностью до округления).
Осталось понять, как выбирать такие множества . Будем выбирать в качестве
непрерывные отрезки прямой. Пусть нам известно, что
принадлежит отрезку
(изначально это отрезок
). В следующего множества
возмём отрезок
, где
. Тогда за каждый заплаченный рубль текущий отрезок будет уменьшаться в
раз. Когда длина отрезка станет меньше единицы, мы однозначно определим
. Поэтому цена отгадывания не будет превосходить
Приведённое рассуждение доказывает только верхнюю оценку. Можно доказать и нижнюю оценку: для любого способа задавать вопросы будет такое число , для отгадывания которого придётся заплатить не менее
рублей.
Вероятностный подход: энтропия Шеннона
Вероятностный подход, предложенный Клодом Шенноном в 1948 году, обобщает определение Хартли на случай, когда не все элементы множества являются равнозначными. Вместо множества в этом подходе мы будем рассматривать вероятностное распределение на множестве и оценивать среднее по распределению количество информации, которое содержит случайная величина.
Пусть задана случайная величина , принимающая
различных значений с вероятностями
. Энтропия Шеннона случайной величины
определяется как
(По непрерывности тут нужно доопределить .)
Энтропия Шеннона оценивает среднее количество информации (математическое ожидание), которое содержится в значениях случайной величины.
При первом взгляде на это определение, может показаться совершенно непонятно откуда оно берётся. Шеннон подошёл к этой задаче чисто математически: сформулировал требования к функции и доказал, что это единственная функция, удовлетворяющая сформулированным требованиям.
Я попробую объяснить происхождение этой формулы как обобщение информации по Хартли. Нам бы хотелось, чтобы это определение согласовывалось с определением Хартли, т.е. должны выполняться следующие «граничные условия»:
Будем искать в виде математического ожидания количества информации, которую мы получаем от каждого возможного значения
.
Как оценить, сколько информации содержится в событии ? Пусть
— всё пространство элементарных исходов. Тогда событие
соответствует множеству элементарных исходов меры
. Если произошло событие
, то размер множества согласованных с этим событием элементарных исходов уменьшается с
до
, т.е. событие
сообщает нам
битов информации. Тут мы пользуемся тем, что количество информации в сообщении, которое уменьшает размер пространство поиска в
раз приносит
битов информации.
Примеры
Свойства энтропии Шеннона
Для случайной величины , принимающей
значений с вероятностями
, выполняются следующие соотношения.
-
.
-
распределение
вырождено.
-
.
-
распределение
равномерно.
Чем распределение ближе к равномерному, тем больше энтропия Шеннона.
Энтропия пары
Понятие энтропии Шеннона можно обобщить для пары случайных величин. Аналогично это обощается для тройки, четвёрки и т.д.
Пусть совместно распределённые случайные величины и
принимают значения
и
, соответственно. Энтропия пары случайных величин
и
определяется следующим соотношением:
Примеры
Рассмотрим эксперимент с выбрасыванием двух игральных кубиков — синего и красного.
Свойства энтропии Шеннона пары случайных величин
Для энтропии пары выполняются следующие свойства.
Условная энтропия Шеннона
Теперь давайте научимся вычислять условную энтропию одной случайной величины относительно другой.
Условная энтропия относительно
определяется следующим соотношением:
Примеры
Рассмотрим снова примеры про два игральных кубика.
Свойства условной энтропии
Условная энтропия обладает следующими свойствами
Взаимная информация
Ещё одна информационная величина, которую мы введём в этом разделе — это взаимная информация двух случайных величин.
Информация в о величине
(взаимная информация случайных величин
и
) определяется следующим соотношением
Примеры
И снова обратимся к примерам с двумя игральными кубиками.
Свойства взаимной информации
Выполняются следующие соотношения.
-
. Т.е. определение взаимной информации симметрично и его можно переписать так:
-
Или так:
.
-
и
.
-
.
-
.
Все информационные величины, которые мы определили к этому моменту можно проиллюстрировать при помощи кругов Эйлера.
Мы пойдём дальше и рассмотрим информационную величину, зависящую от трёх случайных величин.
Пусть ,
и
совместно распределены. Информация в
о
при условии
определяется следующим соотношением:
Свойства такие же как и обычной взаимной информации, нужно только добавить соответствующее условие ко всем членам.
Всё, что мы успели определить можно удобно проиллюстрировать при помощи трёх кругов Эйлера.
Из этой иллюстрации можно вывести все определения и соотношения на информационные величины.
Мы не будем продолжать дальше и рассматривать четыре случайные величины по трём причинам. Во-первых, рисовать четыре круга Эйлера со всеми возможными областями — это непросто. Во-вторых, для двух и трёх случайных величин почти все возможные соотношения можно вывести из кругов Эйлера, а для четырёх случайных величин это уже не так. И в третьих, уже для трёх случайных величин возникают неприятные эффекты, демонстрирующие, что дальше будет хуже.
Рассмотрим треугольник в пересечении всех трёх кругов ,
и
. Этот треугольник соответствуют взаимной информации трёх случайных величин
. Проблема с этой информационной величиной заключается в том, что ей не удаётся придать какой-то «физический» смысл. Более того, в отличие от всех остальных величин на картинке
может быть отрицательной!
Рассмотрим пример трёх случайных величин равномерно распределённых на . Пусть
и
будут независимы, а
. Легко проверить, что
. При этом
. В то же время
. Получается следующая картинка.
Мы знаем, что . При этом
. Получается, что
, а
, т.е. для таких случайных величин
.
Применение энтропии Шеннона: кодирование
В этом разделе мы обсудим, как энтропия Шеннона возникает в теории кодирования. Будем рассматривать коды, которые кодируют каждый символ по отдельности.
Пусть задан алфавит . Код — это отображение из
в
. Код
называется однозначно декодируемым, если любое сообщение, полученное применением
к символам некоторого текста, декодируется однозначно.
Код называется префиксным (prefix-free), если нет двух символов и
таких, что
является префиксом
.
Префиксные коды являются однозначно декодируемыми. Действительно, при декодировании префиксного кода легко понять, где находятся границы кодов отдельных символов.
Теорема [Шеннон]. Для любого однозначно декодируемого кода существует префиксный код с теми же длинами кодов символов.
Таким образом для изучения однозначно декодируемых кодов достаточно рассматривать только префиксные коды.
Задача об оптимальном кодировании.
Дан текст . Нужно найти такой код
, что
Пусть . Обозначим через
частоту, с которой символ
встречается в
. Тогда выражение выше можно переписать как
Следующая теорема могла встречаться вам в курсе алгоритмов.
Теорема [Хаффман]. Код Хаффмана, построенный по , является оптимальным префиксным кодом.
Алгоритм Хаффмана по набору частот эффективно строит оптимальный код для задачи оптимального кодирования.
Связь с энтропией
Имеют место две следующие оценки.
Теорема [Шеннон]. Для любого однозначно декодируемого кода выполняется
Теорема [Шеннон]. Для любых значений существует префиксный код
, такой что
Рассмотрим случайную величину , равномерно распределённую на символах текста
. Получим, что
. Таким образом, эти две теоремы задают оценку на среднюю длину кода символа при оптимальном кодировании, т.е. и для кодирования Хаффмана.
Следовательно, длину кода Хаффмана текста можно оценить, как
Применение энтропии Шеннона: шифрования с закрытым ключом
Рассмотрим простейшую схему шифрования с закрытым ключом. Шифрование сообщения с ключом шифрования
выполняется при помощи алгоритма шифрования
. В результате получается шифрограмма
. Зная
получатель шифрограммы восстанавливает исходное сообщение
:
.
Мы будем анализировать эту схему с помощью аппарата энтропии Шеннона. Пусть и
являются случайными величинами. Противник не знает
и
, но знает
, которая так же является случайной величиной.
Для совершенной схемы шифрования (perfect secrecy) выполняются следующие соотношения:
-
, т.е. шифрограмма однозначно определяется по ключу и сообщению.
-
, т.е. исходное сообщение однозначно восстанавливается по шифрограмме и ключу.
-
, т.е. в отсутствие ключа из шифрограммы нельзя получить никакой информации о пересылаемом сообщении.
Теорема [Шеннон]. , даже если условие
нарушается (т.е. алгоритм
использует случайные биты).
Эта теорема утверждает, что для совершенной схемы шифрования длина ключа должна быть не менее длины сообщения. Другими словами, если вы хотите зашифровать и передать своему знакомому файл размера 1Гб, то для этого вы заранее должны встретиться и обменяться закрытым ключом размера не менее 1Гб. И конечно, этот ключ можно использовать только однажды. Таким образом, самая оптимальная совершенная схема шифрования — это «одноразовый блокнот», в котором длина ключа совпадает с длиной сообщения.
Если же вы используете ключ, который короче пересылаемого сообщения, то шифрограмма раскрывает некоторую информацию о зашифрованном сообщении. Причём количество этой информации можно оценить, как разницу между энтропией сообщения и энтропией ключа. Если вы используете пароль из 10 символов при пересылке файла размера 1Гб, то вы разглашаете примерно 1Гб – 10 байт.
Это всё звучит очень печально, но не всё так плохо. Мы ведь никак не учитываем вычислительную мощь противника, т.е. мы не ограничиваем количество времени, которое противнику потребуется на выделение этой информации.
Современная криптография строится на предположении об ограниченности вычислительных возможностей противника. Тут есть свои проблемы, а именно отсутствие математического доказательства криптографической стойкости (все доказательства строятся на различных предположениях), так что может оказаться, что вся эта криптография бесполезна (подробнее можно почитать в статье о мирах Рассела Импальяццо, которая переведена на хабре), но это уже совсем другая история.
Доказательство. Нарисуем картинку для трёх случайных величин и отметим то, что нам известно.
-
.
-
, следовательно
, а значит
.
-
(по свойству взаимной информации), следовательно
, а значит
.
-
. Таким образом,
В доказательстве мы действительно не воспользовались тем, что .
Алгоритмический подход: колмогоровская сложность
Подход Шеннона хорош для случайных величин, но если мы попробуем применить его к текстам, то выходит, что количество информации в тексте зависит только от частот символов, но не зависит от их порядка. При таком подходе получается, что в «Войне и мире» и в тексте, который получается сортировкой всех знаков в «Войне и мире», содержится одинаковое количество информации. Колмогоров предложил подход, позволяющий измерять количество информации в конкретных объектах (строках), а не в случайных величинах.
Внимание. До этого момента я старался следить за математической строгостью формулировок. Для того, чтобы двигаться дальше в том же ключе, мне потребовалось бы предположить, что читатель неплохо знаком с математической логикой и теорией вычислимости. Я пойду более простым путём и просто буду махать руками, заметая под ковёр некоторые подробности. Однако, все утверждения и рассуждения дальше можно математически строго сформулировать и доказать.
Нам потребуется зафиксировать способ описания битовой строки. Чтобы не углубляться в рассуждения про машины Тьюринга, мы будем описывать строки на языках программирования. Нужно только сделать оговорку, что программы на этих языках будут запускаться на компьютере с неограниченным объёмом оперативной памяти (иначе мы получили бы более слабую вычислительную модель, чем машина Тьюринга).
Сложностью строки
относительно языка программирования
называется длина кратчайшей программы, которая выводит
.
Таким образом сложность «Войны и мира» относительноя языка Python — это длина кратчайшей программы на Python, которая печатает текст «Войны и мира». Естественным образом сложность отсортированной версии «Войны и мира» относительно языка Python получится значительно меньше, т.к. её можно предварительно закодировать при помощи RLE.
Сравнение языков программирования
Дальше нам потребуется научиться любимой забаве всех программистов — сравнению языков программирования.
Будем говорить, что язык не хуже языка программирования
и обозначать
, если существует константа
такая, что для для всех
выполняется
Исходя из этого определения получается, что язык Python не хуже (!) этого вашего Haskell! И я это докажу. В качестве константы мы возьмём длину реализации интепретатора Haskell на Python. Таким образом, любая программа на Haskell переделывается в программу на Python просто дописыванием к ней интерпретатора Haskell на Python.
Соломонов и Колмогоров пошли дальше и доказали существования оптимального языка программирования.
Теорема [Соломонова-Колмогорова]. Существует способ описания (язык программирования) такой, что для любого другого способа описания
выполняется
.
И да, некоторые уже наверное догадались, что — это JavaScript. Или любой другой Тьюринг полный язык программирования.
Это приводит нас к следующему определению, предложенному Колмогоровым в 1965 году.
Колмогоровской сложностью строки будем называть её сложность относительно оптимального способа описания
и будем обозначать
.
Важно понимать, что при разных выборах оптимального языка программирования колмогоровская сложность будет отличаться, но только на константу. Для любых двух оптимальных языков программирования
и
выполняется
и
, т.е. существует такая константа
, что
Это объясняет, почему в этой науке аддитивные константы принято игнорировать.
При этом для конкретной строки и конкретного выбора колмогоровская сложность определена однозначно.
Свойства колмогоровской сложности
Начнём с простых свойств. Колмогоровская сложность обладает следующими свойствами.
Первое свойство выполняется потому, что мы всегда можем зашить строку в саму программу. Второе свойство верно, т.к. из программы, выводящей строку , легко сделать программу, которая выводит эту строку дважды.
Примеры
Несжимаемые строки
Важнейшее свойство колмогоровской сложности заключается в существовании сложных (несжимаемых строк). Проверьте себя и попробуйте объяснить, почему не бывает идеальных архиваторов, которые умели бы сжимать любые файлы хотя бы на 1 байт, и при этом позволяли бы однозначно разархивировать результат.
В терминах колмогоровской сложности это можно сформулировать так.
Вопрос. Существует ли такая длина строки
, что для любой строки
колмогоровская сложность
меньше
?
Следующая теорема даёт отрицательный ответ на этот вопрос.
Теорема. Для любого существует
такой, что
.
Доказательство. Битовых строк длины всего
. Число строк сложности меньше
не превосходит число программ длины меньше
, т.е. таких программ не больше чем
Таким образом, для какой-то строки гарантированно не хватит программы.
Верна и более сильная теорема.
Теорема. Существует такое, что для
слов длины
верно
Другими словами, почти все строки длины имеют почти максимальную сложность.
Колмогоровская сложность: вычислимость
В этом разделе мы поговорим про вычислимость колмогоровской сложности. Я не буду давать формально определение вычислимости, а буду опираться на интуитивные предствления читателей.
Теорема. Не существует программы, которая по двоичной записи числа выводит строку
, такую что
.
Эта теорема говорит о том, что не существует программы-генератора, которая умела бы генерировать сложные строки по запросу.
Доказательство. Проведём доказетельство от противного. Пусть такая программа существует и
. Тогда с одной стороны сложность
не меньше
, а с другой стороны мы можем описать
при помощи
битов и кода программы
.
Это приводит нас к противоречию, т.к. при достаточно больших значениях неизбежно станет больше, чем
.
Как следствие мы получаем невычислимость колмогоровской сложности.
Следствие. Отображение не является вычислимым.
Опять же, предположим, что это нет так и существует программа , которая по строку вычисляет её колмогоровскую сложность. Тогда на основе программы
можно реализовать программу
из теоремы выше: она будет перебирать все строки длины не более
и находить лексикографически первую, для которой сложность будет не меньше
. А мы уже доказали, что такой программы не существует.
Связь с энтропией Шеннона
Теорема. Пусть длины
содержит
единиц и
нулей, тогда
Я надеюсь, что вы уже узнали энтропию Шеннона для случайной величины с двумя значениями с вероятностями и
.
Для колмогоровской сложности можно проделать весь путь, который мы проделали для энтропии Шеннона: определить условную колмогоровскую сложность, сложность пары строк, взаимную информацию и условную взаимную информацию и т.д. При этом формулы будут повторять формулы для энтропии Шеннона с точностью до . Однако это тема для отдельной статьи.
Применение колмогоровской сложности: бесконечность множества простых чисел
Начнём с довольно игрушечного применения. С помощью колмогоровской сложности мы докажем следующую теорему, знакомую нам со школы.
Теорема. Простых чисел бесконечно много.
Очевидно, что для доказательства этой теоремы никакая колмогоровская сложность не нужна. Однако на этом примере я смогу продемонстрировать основные идеи применения колмогоровской сложности в более сложных ситуациях.
Доказательство. Проведём доказательство от обратного. Пусть существует всего простых чисел:
. Тогда любое натуральное
раскладывается на степени простых:
т.е. определяется набором степеней . Каждое
, т.е. задаётся
битами. Поэтому любое
можно задать при помощи
битов (помним, что
— это константа).
Теперь воспользуемся теоремой о существовании несжимаемых строк. Как следствие, мы можем заключить, что существуют -битовые числа
сложности не менее
(можно взять сложную строку и приписать в начало единицу). Получается, что сложное число можно задать при помощи небольшого числа битов.
Противоречие.
Применение колмогоровской сложности: алгоритмическая случайность
Колмогоровская сложность позволяет решить следующую проблему из классической теории вероятностей.
Пусть в лаборатории живёт обезьянка, которую научили печатать на печатной машинке так, что каждую кнопку она нажимает с одинаковой вероятность. Вам предлагается посмотреть на лист печатного текста и сказать, верите ли вы, что его напечатала эта обезьянка. Вы смотрите на лист и видите, что это первая страница «Гамлета» Шекспира. Поверите ли вы? Очевидно, что нет. Хорошо, а если это не Шекспир, а, скажем, текст детектива Дарьи Донцовой? Скорей всего тоже не поверите. А если просто какой-то набор русских слов? Опять же, очень сомневаюсь, что вы поверите.
Внимание, вопрос. А как объяснить, почему вы не верите? Давайте для простоты считать, что на странице помещается 2000 знаков и всего на машинке есть 80 знаков. Вы можете резонно заметить, что вероятность того, что обезьянка случайным образом породила текст «Гамлета» порядка , что астрономически мало. Это верно.
Теперь предположим, что вам показали текст, который вас устроил (он с вашей точки зрения будет похож на «случайный»). Но ведь вероятность его появления тоже будет порядка . Как же вы определяете, что один текст выглядит «случайным», а другой — не выглядит?
Колмогоровская сложность позволяет дать формальный ответ на этот вопрос. Если у текста отстутствует короткое описание (т.е. в нём нет каких-то закономерностей, которые можно было бы использовать для сжатия), то такую строку можно назвать случайной. И как мы увидели выше почти все строки имеют большую колмогоровскую сложность. Поэтому, когда вы видите строку с закономерностями, т.е. маленькой колмогоровской сложности, то это соответствует очень редкому событию. В противоположность наблюдению строки без закономерностей. Вероятность увидеть строку без закономерностей близка к 1.
Это обобщается на случай бесконечных последовательностей. Пусть . Как определить понятие случайной последовательности?
(неформальное определение)
Последовательность случайна по Мартину–Лёфу, если каждый её префикс является несжимаемым.
Оказывается, что это очень хорошее определение случайных последовательностей, т.к. оно обладает ожидаемыми свойствами.
Свойства случайных последовательностей
-
Почти все последовательности являются случайными по Мартину–Лёфу, а мера неслучайных равна
.
-
Всякая случайная по Мартину-Лёфу последовательность невычислима.
-
Если
случайная по Мартин-Лёфу, то
Заключение
Если вам интересно изучить эту тему подробнее, то я рекомендую обратиться к следующим источникам.
-
Верещагин Н.К., Щепин Е.В. Информация, кодирование и предсказание. МЦНМО. (нет в свободном доступе, но pdf продаётся за копейки)
-
В.А. Успенский, А.Х. Шень, Н.К. Верещагин. Колмогоровская сложность и алгоритмическая случайность.
-
Курс «Введение в теорию информации» А.Е. Ромащенко в Computer Science клубе.
Если вам интересны подобные материалы, подписывайтесь в соцсетях на CS клуб и CS центр, а так же на наши каналы на youtube: CS клуб, CS центр.
Измерение информации

4.4
Средняя оценка: 4.4
Всего получено оценок: 618.
4.4
Средняя оценка: 4.4
Всего получено оценок: 618.
Как и любую другую физическую величину, информацию можно измерить. Существуют разные подходы к измерению информации. Один из таких подходов рассматривается в курсе информатики за 7 класс.
Что такое измерение информации
При измерении информации следует учитывать как объем передаваемого сообщения, так и его смысловую нагрузку. В связи с этим в информатике существуют разные подходы к измерению информации.
Алфавитный подход к измерению информации
Способы оценки величины информации могут учитывать или не учитывать смысла информационного сообщения.
Один из способов нахождения количества информации основан на определении веса каждого символа в тексте сообщения. При таком подходе объем сообщения зависит от количества знаков в тексте, чем больше тест, тем больше весит информационное сообщение. При этом абсолютно не важно, что написано, какой смысл несет сообщение. Так как определение объема информации привязано к текстовым единицам: буквам, цифрам, знакам препинания, то такой подход к измерению информации получил название алфавитного.
Вес отдельного знака зависит от их количества в алфавите. Число символов алфавита называют мощностью (N). Например, мощность алфавита английского языка по числу символов равно 26, русского языка 33. Но на самом деле, при написании текста используются и прописные и строчные буквы, а также знаки препинания, пробелы и специальные невидимые символы, обозначающие конец абзаца и перевод к новой строке. Поэтому имеют дело с мощностью 128 или в расширенной версии 256 символов.
Бит, байт и другие единицы измерения
Для двоичного алфавита, состоящего из двух символов – нуля и единицы, мощность алфавита будет составлять 2. Вес символа бинарного алфавита выбран в качестве минимальной единицы информации и называется «бит». Происхождение термина «бит» исходит от англоязычного слова «binary», что означает двоичный.
Восемь бит образуют байт.
Название «байт» было придумано в 1956 году В. Бухгольцем при проектировании первого суперкомпьютера. Слово «byte» было получено путем замены второй буквы в созвучном слове «bite», чтобы избежать путаницы с уже имеющимся термином «bit».
На практике величина объема информации выражает в более крупных единицах: килобайтах, терабайтах, мегабайтах.
Следует запомнить, что килобайт равен 1024 байта, а не 1000. Как, например, 1 километр равен 1000 метрам. Эта разница получается за счет того, 1 байт равен 8 битам, а не 10.
Для того, чтобы легче запомнить единицы измерения, следует воспользоваться таблицей степени двойки.
Таблица степеней двойки
|
Показатель степени |
Значение |
|
1 |
2 |
|
2 |
4 |
|
3 |
8 |
|
4 |
16 |
|
5 |
32 |
|
6 |
64 |
|
7 |
128 |
|
8 |
256 |
|
9 |
512 |
|
10 |
1024 |
|
20 |
1048576 |
То есть, 23 = 8 – это 1 байт, состоящий из 8 бит, 210 = 1024 это 1 килобайт, 220 = 1048576 представляет собой 1 мегабайт, 230 = 1 гигабайт, 240 = 1 терабайт.
Определение количества информации
Вес символа (i) и мощность алфавита (N) связаны между собой соотношением: 2i = N.
Так, алфавит мощностью в 256 символов имеет вес каждого символа в 8 бит, то есть один байт. Это означает, что на каждую букву приходится по байту. В таком случае, нетрудно определить, сколько весит весь кодируемый текст сообщения. Для этого достаточно вес символа алфавита умножить на количество символов в тексте. При подсчете количества символов в сообщении следует не забывать, что знаки препинания, а также пробелы – это тоже символы и они весят столько же, сколько и буквы.
Например, при условии, что каждая буква кодируется одним байтом, для текста, «Ура! Наступили каникулы.» информационный объем определяется умножением 8 битов на 24 символа (без учета кавычек). Произведение 8 * 24 = 192 бита – столько весит кодируемая фраза. В переводе на байты: 192 бита разделить на 8 получим 24 байта.
Эта схема работает и в обратной задаче. Пусть информационное сообщение составляет 2 килобайта и состоит из 512 символов. Необходимо определить мощность алфавита, используемого для кодирования сообщения.
Решение: Сначала целесообразно 2 килобайта перевести в биты: 2 * 1024 = 2048 (бит). Затем объем информационного сообщения делят на количество символов: 2048 / 512 = 4 (бит), получают вес одного символа. Для определения мощности алфавита 2 возводят в степень 4 и получают 16 – это мощность алфавита, то есть количество символов, используемых для кодирования текста.
Что мы узнали?
Одним из способов определения величины информационного сообщения является алфавитный подход, в котором любой знак в тексте имеет некоторый вес, обусловленный мощностью алфавита. Минимальной единицей измерения информации является бит. Информацию можно также измерять в байтах, килобайтах, мегабайтах.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
-
Назар Василенко
7/10
-
Анастасия Арапова
9/10
Оценка статьи
4.4
Средняя оценка: 4.4
Всего получено оценок: 618.
А какая ваша оценка?
|
Измерение информации
|
Информатика, 10 класс. Урок № 2.
Тема — Подходы к измерению информации
Перечень вопросов, рассматриваемых в теме: Информация как снятая неопределенность. Содержательный подход к измерению информации.
Информация как последовательность символов некоторого алфавита. Алфавитный подход к измерению информации. Единицы измерения информации. Понятие больших данных
Глоссарий по теме: Информатика, информация, свойства информации (объективность, достоверность, полнота, актуальность, понятность, релевантность), виды информации, информационные процессы, информационная культура, информационная грамотность.
Основная литература по теме урока:
Л. Л. Босова, А. Ю. Босова. Информатика. Базовый уровень: учебник для 10 класса — М.: БИНОМ. Лаборатория знаний, 2017
Дополнительная литература по теме урока:
И. Г. Семакин, Т. Ю. Шеина, Л. В. Шестакова. Информатика и ИКТ. Профильный уровень: учебник для 10 класса — М.: БИНОМ. Лаборатория знаний, 2012
Теоретический материал для самостоятельного изучения:
Давайте составим план, что бы мы хотели сделать с имеющейся у нас информацией.
Хранить? — возможно.
Передавать — скорее всего, а может быть даже и продавать.
Обрабатывать и получать новую — вполне возможно!
Во всех трех случаях, которые называют основными информационными процессами, нам нужно информацию измерять.
В случае хранения, чтобы быть уверенными, что объем хранилища и объем нашей информации соответствуют друг другу, в передаче или продаже — чтобы объем продажи соответствовал цене, в случае обработки, чтобы рассчитать время, за которое этот объем может быть обработан.
Во всех трех случаях мы говорим о соответствиях объемов, но если нам известно как вычислить объем хранилища в м3, количество денег в рублях или иной валюте, время, то с вычислением объема информации нужно разбираться
Целью нашего урока будет определить способы измерения информации и сравнить их.
Задачи
Для этого нужно будет определить:
— от чего зависит объем информации,
— какими единицами ее измерять.
Ожидаемые результаты
Выявлять различия в подходах к измерению информации.
Применять различные подходы для измерения количества информации.
Переходить от одних единиц измерения информации к другим.
Предположим, что объем информации зависит от ее содержания. Нам нужна информация, которая для нас нова и понятна, соответствует всем свойствам информации, то есть та, которая приносит нам новые знания, решает наши вопросы.
Тут минимальным количеством информации будет ответ «да» или «нет». Ответ на такой простой вопрос принесет нам минимум информации и уменьшит неопределенность в два раза. Было два варианта, мы выбрали один и получили минимум информации — 1 бит.
Этот подход к измерению предложил К. Шеннон.
Информация (по Шеннону) — это снятая неопределённость. Величина неопределённости некоторого события — это количество возможных результатов (исходов) данного события. Сообщение, уменьшающее неопределённость знания в 2 раза, несёт 1 бит информации. Количество информации (i), содержащееся в сообщении об одном из N равновероятных результатов некоторого события, определяется из решения уравнения: 2i = N. Такой подход к измерению информации называют содержательным.
Разумно так же предположить, что текст, который для вас не понятен, понятен кому-то другому, то есть информация в нем все-таки есть. А ее объем зависит не от содержания текста, а от символов, которыми он написан. Назовем алфавитом все множество символов, используемых в языке, а их количество — мощностью алфавита.
Каждый символ, выбранный из алфавита, несет количество информации (i), вычисленное по формуле,
где N мощность алфавита.
Общее количество информации (I) во всем тексте можно посчитать по простой математической модели:
где k — количество символов в тексте.
Такой подход к измерению информации называют алфавитным. Здесь объем информации зависит от используемого алфавита и количества символов в тексте.
Этот подход к измерению информации предложил советский ученый-математик А. Н. Колмогоров.
Бит — мельчайшая единица информации. Для кодировки каждого из 256 символов, сведенных в таблицу кодировки ASCII, требуется 8 бит. Эта величина получила отдельное название — байт. Помимо бита и байта существуют более крупные единицы. Традиционно они получили приставки Кило, Мега, Гига и т. д.
Но Кило в единицах измерения информации обозначает не 103=1000, а 210=1024. Это недоразумение решается с конца XX века. Международная электротехническая комиссия предложила приставки «киби-, меби-, гиби-», которые лучше отражают смысл кратности степеням двойки.
Переводить единицы измерения информации можно при помощи удобной схемы
Определив подходы и единицы измерения, перейдем к оценкам. Сколько информации содержит книга? Библиотека? Видеоролик? Много? Это конечно, можно посчитать по уже известным нам простым формулам, а вот оценить «много» или «мало» не удастся, потому что это не количественные категории.
Сегодня существует понятие «большие данные». Так называют социально-экономический феномен, связанный с появлением технологических возможностей анализировать огромные массивы данных. Эти технологические возможности стремительно развиваются и уже позволяют компьютерам узнавать нас на фото, советуют нам какую музыку слушать и какие книги читать. Такси безошибочно находит нас в большом городе и проходит тестирование беспилотный транспорт.
Объемы данных, которыми оперирует человечество, исчисляется единицами зеттабайт, это единицы и 61 «0», к 2020 году по прогнозам это будет 40—44 зеттабайтов, а 2025 возрастет в 10 раз. Данные станут жизненно-важным активом, а их безопасность — критически важным вопросом.
Подведем итоги
Информацию можно измерять. Для этого существуют разные подходы, содержательный подход, алфавитный подход.
Суть содержательного подхода в том, что при определении объема информации учитывается содержание информации. Она должна быть новой и понятной получателю.
Суть алфавитного подхода в определении количества информации в зависимости от алфавита, которым она записана. А объем подсчитывается по формуле
где — объем информации,
— количество символов в сообщении,
— количество информации о каждом символе.
Для измерения количества информации в объеме данных используются единицы измерения информации.
Обработка данных важна для всех сфер жизни. Технологии обработки данных стремительно развиваются и становятся жизненно-важными.
За единицу количества информации
принимается такое количество информации,
которое содержит сообщение, уменьшающее
неопределенность в два раза. Такая
единица названа «бит».
Для информации существуют свои единицы
измерения информации. Если рассматривать
сообщения информации как последовательность
знаков, то их можно представлять битами,
а измерять в байтах, килобайтах,
мегабайтах, гигабайтах, терабайтах и
петабайтах.
Давайте разберемся с этим, ведь нам
придется измерять объем памяти и
быстродействие компьютера.
Бит
Единицей измерения количества информации
является бит – это наименьшая
(элементарная) единица.
1бит – это количество информации,
содержащейся в сообщении, которое вдвое
уменьшает неопределенность знаний о
чем-либо.
Байт
Байт – основная единица измерения
количества информации.
Байтом называется последовательность
из 8 битов.
Байт – довольно мелкая единица измерения
информации. Например, 1 символ – это 1
байт.
Производные единицы измерения количества
информации
1 байт=8 битов
1 килобайт (Кб)=1024 байта =210 байтов
1 мегабайт (Мб)=1024 килобайта =210 килобайтов=220
байтов
1 гигабайт (Гб)=1024 мегабайта =210 мегабайтов=230
байтов
1 терабайт (Гб)=1024 гигабайта =210 гигабайтов=240
байтов
Запомните, приставка КИЛО в информатике
– это не 1000, а 1024, то есть 210 .
Методы измерения количества информации
Итак, количество информации в 1 бит вдвое
уменьшает неопределенность знаний.
Связь же между количеством возможных
событий N и количеством информации I
определяется формулой Хартли:
N=2i.
Алфавитный подход к измерению количества
информации
При этом подходе отвлекаются от содержания
(смысла) информации и рассматривают ее
как последовательность знаков определенной
знаковой системы. Набор символов языка,
т.е. его алфавит можно рассматривать
как различные возможные события. Тогда,
если считать, что появление символов в
сообщении равновероятно, по формуле
Хартли можно рассчитать, какое количество
информации несет в себе каждый символ:
I=log2N.
Вероятностный подход к измерению
количества информации
Этот подход применяют, когда возможные
события имеют различные вероятности
реализации. В этом случае количество
информации определяют по формуле
Шеннона:
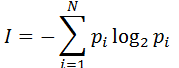
где
I – количество информации,
N – количество возможных событий,
Pi – вероятность i-го события.
6. Кодирование информации различных видов
1.6.1. КОДИРОВАНИЕ ЧИСЕЛ.
Используя n бит, можно записывать двоичные
коды чисел от 0 до 2n-1, всего 2n чисел.
1) Кодирование положительных чисел: Для
записи положительных чисел в байте
заданное число слева дополняют нулями
до восьми цифр. Эти нули называют
незначимыми.
Например: записать в байте число 1310 =
11012
Результат: 00001101
2) Кодирование отрицательных чисел:Наибольшее
положительное число, которое можно
записать в байт, — это 127, поэтому для
записи отрицательных чисел используют
числа с 128-го по 255-е. В этом случае, чтобы
записать отрицательное число, к нему
добавляют 256, и полученное число записывают
в ячейку.
1.6.2. КОДИРОВАНИЕ ТЕКСТА.
Соответствие между набором букв и
числами называется кодировкой символа.
Как правило, код символа хранится в
одном байте, поэтому коды символов могут
принимать значение от 0 до 255. Такие
кодировки называют однобайтными. Они
позволяют использовать 256 символов.
Таблица кодов символов называется ASCII
(American StandardCodeforInformationInterchange- Американский
стандартный код для обмена информацией).
Таблица ASCII-кодов состоит из двух частей:
Коды от 0 до 127 одинаковы для всех IBM-PC
совместимых компьютеров и содержат:
коды управляющих символов;
коды цифр, арифметических операций,
знаков препинания;
некоторые специальные символы;
коды больших и маленьких латинских
букв.
Вторая часть таблицы (коды от 128 до 255)
бывает различной в различных компьютерах.
Она содержит:
коды букв национального алфавита;
коды некоторых математическихсимволов;
коды символов псевдографики.
В настоящее время все большее
распространение приобретает двухбайтная
кодировка Unicode. В ней коды символов могут
принимать значение от 0 до 65535.
1.6.3. КОДИРОВАНИЕ ЦВЕТОВОЙ ИНФОРМАЦИИ.
Одним байтом можно закодировать 256
различных цветов. Это достаточно для
рисованных изображений типа мультфильмов,
но не достаточно для полноцветных
изображений живой природы. Если для
кодирования цвета использовать 2 байта,
можно закодировать уже 65536 цветов. А
если 3 байта – 16,5 млн. различных цветов.
Такой режим позволяет хранить, обрабатывать
и передавать изображения, не уступающие
по качеству наблюдаемым в живой природе.
Из курса физики известно, что любой цвет
можно представить в виде комбинации
трех основных цветов: красного, зеленого,
синего (их называют цветовыми
составляющими). Если кодировать цвет
точки с помощью 3 байтов, то первый байт
выделяется красной составляющей, второй
– зеленой, третий – синей. Чем больше
значение байта цветовой составляющей,
тем ярче этот цвет.
Белый цвет – у точки есть все цветовые
составляющие, и они имеют полную яркость.
Поэтому белый цвет кодируется так: 255
255 255. (11111111 11111111 11111111)
Черный цвет – отсутствие всех прочих
цветов: 0 0 0. (00000000 00000000 00000000)
Серый цвет – промежуточный между черным
и белым. В нем есть все цветовые
составляющие, но они одинаковы и
нейтрализуют друг друга.
Например: 100 100 100 или 150 150 150. (2-й вариант
— ярче).
Красный цвет – все составляющие, кроме
красной, равны 0. Темно-красный: 128 0 0.
Ярко-красный: 255 0 0.
Зеленый цвет – 0 255 0.
Синий цвет – 0 0 255.
1.6.4. КОДИРОВАНИЕ ГРАФИЧЕСКОЙ ИНФОРМАЦИИ.
Рисунок разбивают на точки. Чем больше
будет точек, и чем мельче они будут, тем
точнее будет передача рисунка. Затем,
двигаясь по строкам слева направо
начиная с верхнего левого угла,
последовательно кодируют цвет каждой
точки. Для черно-белой картинки достаточно
1 байта для точки, для цветной – до 3-х
байт для одной точки.
Двоичная система счисления
В двоичной системе счисления используются
всего две цифры 0 и 1. Другими словами,
двойка является основанием двоичной
системы счисления. (Аналогично у
десятичной системы основание 10.)
Чтобы научиться понимать числа в двоичной
системе счисления, сначала рассмотрим,
как формируются числа в привычной для
нас десятичной системе счисления.
В десятичной системе счисления мы
располагаем десятью знаками-цифрами
(от 0 до 9). Когда счет достигает 9, то
вводится новый разряд (десятки), а единицы
обнуляются и счет начинается снова.
После 19 разряд десятков увеличивается
на 1, а единицы снова обнуляются. И так
далее. Когда десятки доходят до 9, то
потом появляется третий разряд – сотни.
Двоичная система счисления аналогична
десятичной за исключением того, что в
формировании числа участвуют всего
лишь две знака-цифры: 0 и 1. Как только
разряд достигает своего предела (т.е.
единицы), появляется новый разряд, а
старый обнуляется.
Попробуем считать в двоичной системе:
0 – это ноль
1 – это один (и это предел разряда)
10 – это два
11 – это три (и это снова предел)
100 – это четыре
101 – пять
110 – шесть
111 – семь и т.д.
Перевод чисел из двоичной системы
счисления в десятичную
Не трудно заметить, что в двоичной
системе счисления длины чисел с
увеличением значения растут быстрыми
темпами. Как определить, что значит вот
это: 10001001? Непривычный к такой форме
записи чисел человеческий мозг обычно
не может понять сколько это. Неплохо бы
уметь переводить двоичные числа в
десятичные.
В десятичной системе счисления любое
число можно представить в форме суммы
единиц, десяток, сотен и т.д. Например:
1476 = 1000 + 400 + 70 + 6
Можно пойти еще дальше и разложить так:
1476 = 1 * 103 + 4 * 102 + 7 * 101 + 6 * 100
Посмотрите на эту запись внимательно.
Здесь цифры 1, 4, 7 и 6 — это набор цифр из
которых состоит число 1476. Все эти цифры
поочередно умножаются на десять
возведенную в ту или иную степень. Десять
– это основание десятичной системы
счисления. Степень, в которую возводится
десятка – это разряд цифры за минусом
единицы.
Аналогично можно разложить и любое
двоичное число. Только основание здесь
будет 2:
10001001 = 1*27 + 0*26 + 0*25 + 0*24 + 1*23 + 0*22 + 0*21 + 1*20
Если посчитать сумму составляющих, то
в итоге мы получим десятичное число,
соответствующее 10001001:
1*27 + 0*26 + 0*25 + 0*24 + 1*23 + 0*22 + 0*21 + 1*20 = 128 + 0 + 0 +
0 + 8 + 0 + 0 + 1 = 137
Т.е. число 10001001 по основанию 2 равно числу
137 по основанию 10. Записать это можно
так:
100010012 = 13710
Почему двоичная система счисления так
распространена?
Дело в том, что двоичная система счисления
– это язык вычислительной техники.
Каждая цифра должна быть как-то
представлена на физическом носителе.
Если это десятичная система, то придется
создать такое устройство, которое может
быть в десяти состояниях. Это сложно.
Проще изготовить физический элемент,
который может быть лишь в двух состояниях
(например, есть ток или нет тока). Это
одна из основных причин, почему двоичной
системе счисления уделяется столько
внимания.
Перевод десятичного числа в двоичное
Может потребоваться перевести десятичное
число в двоичное. Один из способов –
это деление на два и формирование
двоичного числа из остатков. Например,
нужно получить из числа 77 его двоичную
запись:
77 / 2 = 38 (1 остаток)
38 / 2 = 19 (0 остаток)
19 / 2 = 9 (1 остаток)
9 / 2 = 4 (1 остаток)
4 / 2 = 2 (0 остаток)
2 / 2 = 1 (0 остаток)
1 / 2 = 0 (1 остаток)
Собираем остатки вместе, начиная с
конца: 1001101. Это и есть число 77 в двоичном
представлении. Проверим:
1001101 = 1*26 + 0*25 + 0*24 + 1*23 + 1*22 + 0*21 + 1*20 = 64 + 0 + 0
+ 8 + 4 + 0 + 1 = 77
ASCII(англ. American Standard Code for Information
Interchange) — американская стандартная
кодировочная таблица для печатных
символов и некоторых специальных кодов.
В американском варианте английского
языка произносится [э́ски], тогда как в
Великобритании чаще произносится
[а́ски]; по-русски произносится также
[а́ски] или [аски́].
ASCII представляет собой кодировку для
представления десятичных цифр, латинского
и национального алфавитов, знаков
препинания и управляющих символов.
Изначально разработанная как 7-битная,
с широким распространением 8-битного
байта ASCII стала восприниматься как
половина 8-битной. В компьютерах обычно
используют расширения ASCII с задействованным
8-м битом и второй половиной кодовой
таблицы (например КОИ-8).
Поскольку ASCII изначально предназначался
для обмена информацией (по телетайпу),
в нём, кроме информационных символов,
используются символы-команды для
управления связью. Это обычный набор
спецсигналов, применявшийся и в других
докомпьютерных средствах обмена
сообщениями (азбука Морзе, семафорная
азбука), дополненный с учётом специфики
устройства.
(После названия каждого символа указан
его 16-ричный код)
NUL, 00 — Null, пустой. Всегда игнорировался.
На перфолентах 1 представлялась
отверстием, 0 — отсутствием отверстия.
Поэтому пустые части перфоленты до
начала и после конца сообщения состояли
из таких символов. Сейчас используется
во многих языках программирования как
конец строки. (Строка понимается как
последовательность символов.) В некоторых
операционных системах NUL — последний
символ любого текстового файла.
SOH, 01 — Start Of Heading, начало
заголовка.
STX, 02 — Start of Text, начало
текста. Текстом
называлась часть сообщения, предназначенная
для печати. Адрес, контрольная сумма и
т. д. входили или в заголовок, или в часть
сообщения после текста.
ETX, 03 — End of Text, конец
текста. Здесь телетайп
прекращал печатать. Использование
символа Ctrl-C, имеющего код 03, для прекращения
работы чего-то (обычно программы),
восходит ещё к тем временам.
EOT, 04 — End of Transmission, конец
передачи. В системе
UNIX Ctrl-D, имеющий тот же код, означает
конец файла при вводе с клавиатуры.
ENQ, 05 — Enquire. Прошу
подтверждения.
ACK, 06 — Acknowledgement. Подтверждаю.
BEL, 07 — Bell, звонок, звуковой сигнал. Сейчас
тоже используется. В языках программирования
C и C++ обозначается a.
BS, 08 — Backspace, возврат на один символ.
Сейчас стирает предыдущий символ.
TAB, 09 — Tabulation. Обозначался также HT —
Horizontal Tabulation, горизонтальная табуляция.
Во многих языках программирования
обозначается t .
LF, 0A — Line Feed, перевод строки. Сейчас в
конце каждой строчки текстового файла
ставится либо этот символ, либо CR, либо
и тот и другой (CR, затем LF), в зависимости
от операционной системы. Во многих
языках программирования обозначается
n и при выводе текста приводит к переводу
строки.
VT, 0B — Vertical Tab, вертикальная табуляция.
FF, 0C — Form Feed, прогон страницы, новая
страница.
CR, 0D — Carriage Return, возврат
каретки. Во многих
языках программирования этот символ,
обозначаемый r, можно использовать для
возврата в начало строчки без перевода
строки. В некоторых операционных системах
этот же символ, обозначаемый Ctrl-M, ставится
в конце каждой строчки текстового файла
перед LF.
SO, 0E — Shift Out, измени цвет ленты (использовался
для двуцветных лент; цвет менялся обычно
на красный). В дальнейшем обозначал
начало использования национальной
кодировки.
SI, 0F — Shift In, обратно к Shift Out.
DLE, 10 — Data Link Escape, освобождение канала
данных — следующие символы представляют
собой данные, а не управляющие символы.
DC1, 11 — Device Control 1, 1-й символ управления
устройством — включить устройство
чтения перфоленты.
DC2, 12 — Device Control 2, 2-й символ управления
устройством — включить перфоратор.
DC3, 13 — Device Control 3, 3-й символ управления
устройством — выключить устройство
чтения перфоленты.
DC4, 14 — Device Control 4, 4-й символ управления
устройством — выключить перфоратор.
NAK, 15 — Negative Acknowledgment, не
подтверждаю. Обратно
Acknowledgment.
SYN, 16 — Synchronization. Этот символ передавался,
когда для синхронизации было необходимо
что-нибудь передать.
ETB, 17 — End of Text Block, конец
текстового блока.
Иногда текст по техническим причинам
разбивался на блоки.
CAN, 18 — Cancel, отмена (того, что было передано
ранее).
EM, 19 — End of Medium, конец носителя (кончилась
перфолента и т. д.)
SUB, 1A — Substitute, подставить. Ставится на
месте символа, значение которого было
потеряно или испорчено при передаче.
Сейчас Ctrl-Z используется как конец файла
при вводе с клавиатуры в системах DOS и
Windows. У этой функции нет никакой очевидной
связи с символом SUB.
ESC, 1B — Escape. Следующие за ним символы
имеют какое-то другое значение, отличное
от того, которое определено в ASCII. Обычно
начинал управляющие последовательности.
FS, 1C — File Separator, разделитель файлов.
GS, 1D — Group Separator, разделитель групп.
RS, 1E — Record Separator, разделитель записей.
US, 1F — Unit Separator, разделитель юнитов. То
есть поддерживалось 4 уровня структуризации
данных: сообщение могло состоять из
файлов, файлы из групп, группы из записей,
записи из юнитов.
DEL, 7F — Delete, стереть последний символ.
Символом DEL, состоящим в двоичном коде
из всех единиц, можно было забить любой
символ. Устройства и программы игнорировали
DEL так же, как NUL. Код этого символа
происходит из первых текстовых процессоров
с памятью на перфоленте: в них удаление
символа происходило забиванием его
кода дырочками (обозначавшими логические
единицы).
Растровая и векторная графика
Способы представления изображений в
памяти ЭВМ
Формальное определение компьютерная
(машинная) графика – это создание,
хранение и обработка моделей объектов
и их изображений с помощью ЭВМ. Под
интерактивной компьютерной графикой
понимают раздел компьютерной графики,
изучающий вопросы динамического
управления со стороны пользователя
содержанием изображения, его формой,
размерами и цветом на экране с помощью
интерактивных устройств взаимодействия.
Под компьютерной геометрией понимают
математический аппарат, применяемый в
компьютерной графике.
Необходимо отметить следующую
отличительную черту компьютерных
изображений. Изображения, которые мы
встречаем в нашей повседневной жизни,
реальные картины природы, можно бесконечно
детализировать, выявлять все новые
цвета и оттенки. Изображения, хранящиеся
в памяти компьютера, независимо от
способа их получения и представления,
всегда являются усеченной моделью
картины реального мира. Их детализация
возможна лишь с той степенью, которая
была заложена при их создании или
получении, и их цветовая гамма будет не
шире заранее оговоренной.
Одно и то же изображение может быть
представлено в памяти ЭВМ двумя
принципиально различными способами и
получено два различных типа изображения:
растровое и векторное. Рассмотрим
подробнее эти способы представления
изображений, выделим их основные
параметры и определим их достоинства
и недостатки.
Что такое растровое изображение?
Возьмём фотографию (например, см. рис.
1.1). Конечно, она тоже состоит из маленьких
элементов, но будем считать, что отдельные
элементы мы рассмотреть не можем. Она
представляется для нас, как реальная
картина природы.
Теперь разобьём это изображение на
маленькие квадратики (маленькие, но
всё-таки чётко различимые), и каждый
квадратик закрасим цветом, преобладающим
в нём (на самом деле программы при
оцифровке генерируют некий «средний»
цвет, т. е. если у нас была одна чёрная
точка и одна белая, то квадратик будет
иметь серый цвет).
Как мы видим, изображение стало состоять
из конечного числа квадратиков
определённого цвета. Эти квадратики
называют pixel (от PICture ELement) – пиксел или
пиксель.
Рис. 1.1. Исходное изображение
Теперь каким-либо методом занумеруем
цвета. Конкретная реализация этих
методов нас пока не интересует. Для нас
сейчас важно то, что каждый пиксель на
рисунке стал иметь определённый цвет,
обозначенный цифрой (рис. 1.2).
Рис. 1.2. Фрагмент оцифрованного изображения
и номера цветов
Теперь пойдём по порядку (слева направо
и сверху вниз) и будем в строчку выписывать
номера цветов встречающихся пикселей.
Получится строка примерно следующего
вида:
1 2 8 3 212 45 67 45 127 4 78 225 34 …
Вот эта строка и есть наши оцифрованные
данные. Теперь мы можем сжать их (так
как несжатые графические данные обычно
имеют достаточно большой размер) и
сохранить в файл.
Итак, под растровым (bitmap, raster) понимают
способ представления изображения в
виде совокупности отдельных точек
(пикселей) различных цветов или оттенков.
Это наиболее простой способ представления
изображения, ибо таким образом видит
наш глаз.
Достоинством такого способа является
возможность получения фотореалистичного
изображения высокого качества в различном
цветовом диапазоне. Недостатком –
высокая точность и широкий цветовой
диапазон требуют увеличения объема
файла для хранения изображения и
оперативной памяти для его обработки.
Для векторной графики характерно
разбиение изображения на ряд графических
примитивов – точки, прямые, ломаные,
дуги, полигоны. Таким образом, появляется
возможность хранить не все точки
изображения, а координаты узлов примитивов
и их свойства (цвет, связь с другими
узлами и т. д.).
Вернемся к изображению на рис. 1.1. Взглянем
на него по-другому. На изображении легко
можно выделить множество простых
объектов — отрезки прямых, ломанные,
эллипс, замкнутые кривые. Представим
себе, что пространство рисунка существует
в некоторой координатной системе. Тогда
можно описать это изображение, как
совокупность простых объектов,
вышеперечисленных типов, координаты
узлов которых заданы вектором относительно
точки начала координат (рис. 1.3).
Рис. 1.3. Векторное изображение и узлы
его примитивов
Проще говоря, чтобы компьютер нарисовал
прямую, нужны координаты двух точек,
которые связываются по кратчайшей
прямой. Для дуги задается радиус и т.
д. Таким образом, векторная иллюстрация
– это набор геометрических примитивов.
Важной деталью является то, что объекты
задаются независимо друг от друга и,
следовательно, могут перекрываться
между собой.
При использовании векторного представления
изображение хранится в памяти как база
данных описаний примитивов. Основные
графические примитивы, используемые в
векторных графических редакторах:
точка, прямая, кривая Безье, эллипс
(окружность), полигон (прямоугольник).
Примитив строится вокруг его узлов
(nodes). Координаты узлов задаются
относительно координатной системы
макета.
А изображение будет представлять из
себя массив описаний – нечто типа:
отрезок (20,20-100,80);
окружность(50,40-30);
кривая_Безье (20,20-50,30-100,50).
Каждому узлу приписывается группа
параметров, в зависимости от типа
примитива, которые задают его геометрию
относительно узла. Например, окружность
задается одним узлом и одним параметром
– радиусом. Такой набор параметров,
которые играют роль коэффициентов и
других величин в уравнениях и аналитических
соотношениях объекта данного типа,
называют аналитической моделью примитива.
Отрисовать примитив – значит построить
его геометрическую форму по его параметрам
согласно его аналитической модели.
Векторное изображение может быть легко
масштабировано без потери деталей, так
как это требует пересчета сравнительно
небольшого числа координат узлов. Другой
термин – «object-oriented graphics».
Самой простой аналогией векторного
изображения может служить аппликация.
Все изображение состоит из отдельных
кусочков различной формы и цвета (даже
части растра), «склеенных» между собой.
Понятно, что таким образом трудно
получить фотореалистичное изображение,
так как на нем сложно выделить конечное
число примитивов, однако существенными
достоинствами векторного способа
представления изображения, по сравнению
с растровым, являются:
· векторное изображение может быть
легко масштабировано без потери качества,
так как это требует пересчета сравнительно
небольшого числа координат узлов;
· графические файлы, в которых хранятся
векторные изображения, имеют существенно
меньший, по сравнению с растровыми,
объем (порядка нескольких килобайт).
Сферы применения векторной графики
очень широки. В полиграфике – от создания
красочных иллюстраций до работы со
шрифтами. Все, что мы называем машинной
графикой, 3D-графикой, графическими
средствами компьютерного моделирования
и САПР – все это сферы приоритета
векторной графики, ибо эти ветви дерева
компьютерных наук рассматривают
изображение исключительно с позиции
его математического представления.
Как видно, векторным можно назвать
только способ описания изображения, а
само изображение для нашего глаза всегда
растровое. Таким образом, задачами
векторного графического редактора
являются растровая прорисовка графических
примитивов и предоставление пользователю
сервиса по изменению параметров этих
примитивов. Все изображение представляет
собой базу данных примитивов и параметров
макета (размеры холста, единицы измерения
и т. д.). Отрисовать изображение – значит
выполнить последовательно процедуры
прорисовки всех его деталей.
Для уяснения разницы между растровой
и векторной графикой приведем простой
пример. Вы решили отсканировать Вашу
фотографию размером 10´15 см чтобы затем
обработать и распечатать на цветном
принтере. Для получения приемлемого
качества печати необходимо разрешение
не менее 300 dpi. Считаем:
10 см = 3,9 дюйма; 15 см = 5,9 дюймов.
По вертикали: 3,9 * 300 = 1170 точек.
По горизонтали: 5,9 * 300 = 1770 точек.
Итак, число пикселей растровой матрицы
1170 * 1770 = 2 070 900.
Теперь решим, сколько цветов мы хотим
использовать. Для черно-белого изображения
используют обычно 256 градаций серого
цвета для каждого пикселя, или 1 байт.
Получаем, что для хранения нашего
изображения надо 2 070 900 байт или 1,97 Мб.
Для получения качественного цветного
изображения надо не менее 256 оттенков
для каждого базового цвета. В модели
RGB соответственно их 3: красный, зеленый
и синий. Получаем общее количество байт
– 3 на каждый пиксел. Соответственно,
размер хранимого изображения возрастает
в три раза и составляет 5,92 Мб.
Для создания макета для полиграфии
фотографии сканируют с разрешением 600
dpi, следовательно, размер файла вырастает
еще вчетверо.
С другой стороны, если изображение
состоит из простых объектов, то для его
хранения в векторном виде необходимо
не более нескольких килобайт.
Скачать материал

Скачать материал


- Сейчас обучается 21 человек из 11 регионов




- Сейчас обучается 75 человек из 32 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Подходы к понятию информации и измерению информации. Информационные объекты различных видов. Универсальность дискретного (цифрового) представления информации
-
2 слайд
ИНФОРМАЦИЯ
— фундаментальное понятие науки, поэтому определить его исчерпывающим образом через какие-то более простые понятия невозможно
С позиции человека информация – это содержание разных сообщений, это самые разнообразные сведения, которые человек получает из окружающего мира через свои органы чувств. -
3 слайд
Подходы к понятию информации
-
4 слайд
Существует два подхода к измерению информации:
содержательный (вероятностный);
объемный (алфавитный). -
5 слайд
Содержательный (вероятностный) подход к измерению информации
Количество информации можно рассматривать как меру уменьшения неопределенности знания при получении информационных сообщений. -
6 слайд
Главная формула информатики
связывает между собой количество возможных информационных сообщений N и количество информации I, которое несет полученное сообщение:
N = 2I -
7 слайд
За единицу количества информации принимается такое количество информации, которое содержится в информационном сообщении, уменьшающем неопределенность знания в два раза.
Такая единица названа бит.Бит – наименьшая единица измерения информации.
-
8 слайд
С помощью набора битов можно представить любой знак и любое число. Знаки представляются восьмиразрядными комбинациями битов – байтами.
1байт = 8 битов=23битов
Байт – это 8 битов, рассматриваемые как единое целое, основная единица компьютерных данных. -
9 слайд
Рассмотрим, каково количество комбинаций битов в байте.
Если у нас две двоичные цифры (бита), то число возможных комбинаций из них:
22=4:00, 01, 10, 11Если четыре двоичные цифры (бита), то число возможных комбинаций:
24=16:0000, 0001, 0010, 0011,
0100, 0101, 0110, 0111,
1000, 1001, 1010, 1011,
1100, 1101, 1110, 1111 -
10 слайд
Так как в байте- 8 бит (двоичных цифр), то число возможных комбинаций битов в байте:
28=256
Т.о., байт может принимать одно из 256 значений или комбинаций битов. -
11 слайд
Для измерения информации используются более крупные единицы:
килобайты, мегабайты, гигабайты, терабайты и т.д.1 Кбайт =1 024 байт
1 Мбайт = 1 024 Кбайт
1 Гбайт = 1 024 Мбайт
1 Тбайт = 1 024 Гбайт -
12 слайд
Проведем аналогию с единицами длины:
если 1 бит «соответствует» 1 мм, то:
1 байт – 10 мм = 1см;
1 Кбайт – 1000 см = 10 м;
1 Мбайт – 10 000 м = 10 км;
1 Гбайт – 10 000 км (расстояние от Москвы до Владивостока).
Страница учебника содержит приблизительно 3 Кбайта информации;
1 газета – 150 Кбайт. -
13 слайд
Объемный (алфавитный подход)
к измерению информации
Алфавитный подход позволяет измерить количество информации
в тексте, составленном из символов некоторого алфавита. -
14 слайд
Алфавитный подход
к измерению информации
Это объективный,
количественный метод для измерения информации, циркулирующей в информационной технике. -
15 слайд
Алфавит- множество символов, используемых для представления информации.
Мощность алфавита – число символов в алфавите (его размер) N. -
16 слайд
Например, алфавит десятичной системы счисления – множество цифр- 0,1,2,3,4,5,6,7,8,9.
Мощность этого алфавита – 10.
Компьютерный алфавит, используемый для представления текстов в компьютере, использует 256 символов.
Алфавит двоичной системы кодирования информации имеет всего два символа- 0 и 1.
Алфавиты русского и английского языков имеют различное число букв, их мощности – различны. -
17 слайд
Информационный вес символа (количество информации в одном символе), выраженный в битах (i), и мощность алфавита (N) связаны между собой формулой:
N = 2i
где N – это количество знаков в алфавите знаковой системы или мощность
Тогда информационный вес символа:
i = log2N -
18 слайд
Информационная емкость знаков зависит от их количества в алфавите. Так, информационная емкость буквы в русском алфавите, если не использовать букву «ё», составляет:
32 = 2I ,
I=ln32/ln2=3.46/0.69=5
I = 5 битовВ латинском алфавите 26 букв. Информационная емкость буквы латинского алфавита также 5 битов.
-
19 слайд
Количество информации в сообщении или информационный объём текста- Ic, равен количеству информации, которое несет один символ-I, умноженное на количество символов K в сообщении:
Iс = K * i
БИТ -
20 слайд
Например, в слове «информатика» 11 знаков (К=11), каждый знак в русском алфавите несет информацию 5 битов (I=5), тогда количество информации в слове «информатика» Iс=5х11=55 (битов).
С помощью формулы N = 2I можно определить количество информации, которое несет знак в двоичной знаковой системе: N=2 2=2I 21=2I I=1 бит
Таким образом, в двоичной знаковой системе 1 знак несет 1 бит информации. При двоичном кодировании объем информации равен длине двоичного кода.
Чем большее количество знаков содержит алфавит знаковой системы, тем большее количество информации несет один знак. -
21 слайд
Информационные объекты различных видов
-
22 слайд
Информационный объект – обобщающее понятие, описывающее различные виды объектов; это предметы, процессы, явления материального или нематериального свойства, рассматриваемые с точки зрения их информационных свойств.
Простые информационные объекты:
звук, изображение, текст, число.
Комплексные (структурированные) информационные объекты:
элемент, база данных, таблица, гипертекст, гипермедиа. -
23 слайд
Информационный объект:
обладает определенными потребительскими качествами (т.е. он нужен пользователю);
допускает хранение на цифровых носителях;
допускает выполнение над ним определенных действий путем использования аппаратных и программных средств компьютера. -
-
25 слайд
Универсальность дискретного (цифрового) представления информации.
-
26 слайд
Текстовая информация дискретна – состоит из отдельных знаков
Для обработки текстовой информации на компьютере необходимо представить ее в двоичной знаковой системе. Каждому знаку необходимо поставить в соответствие уникальный 8-битовый двоичный код, значения которого находятся в интервале от 00000000 до 11111111 (в десятичном коде от 0 до 255).
-
27 слайд
Дискретное (цифровое) представление графической информации
Изображение на экране монитора дискретно. Оно составляется из отдельных точек- пикселей.
Пиксель — минимальный участок изображения, которому независимым образом можно задать цвет. -
28 слайд
В процессе дискретизации могут использоваться различные палитры цветов. Каждый цвет можно рассматривать как возможное состояние точки.
Количество цветов N в палитре и количество информации I, необходимое для кодирования цвета каждой точки, вычисляется по формуле:
N = 2I -
29 слайд
Пример
Наиболее распространенными значениями глубины цвета при кодировании цветных изображений являются 4, 8, 16 или 24 бита на точку.
Можно определить количество цветов в 24-битовой палитре: N = 2I = 224 = 16 777 21бит. -
30 слайд
Дискретное (цифровое) представление звуковой информации
Частота дискретизации звука — это количество измерений громкости звука за одну секунду.
Глубина кодирования звука — это количество информации, которое необходимо для кодирования дискретных уровней громкости цифрового звука.
Если известна глубина кодирования, то количество уровней громкости цифрового звука можно рассчитать по формуле
N = 2I -
31 слайд
Дискретное (цифровое) представление видеоинформации
ВИДЕОИНФОРМАЦИЯ -это сочетание звуковой и графической информации. Кроме того, для создания на экране эффекта движения используется дискретная технология быстрой смены статических картинок.
Способ уменьшения объема видео: первый кадр запоминается целиком (ключевой), а в следующих сохраняются только отличия от начального кадра (разностные кадры). -
32 слайд
ЗАДАЧИ
Алфавит племени Мульти состоит из 8 букв. Какое количество информации несёт одна буква этого алфавита?
Ответ: 3 бита.
Сообщение, записанное буквами 64-х символьного алфавита, содержит 20 символов. Какой информационный объём оно несёт?
Ответ: 120 бит. -
33 слайд
ЗАДАЧИ
Племя Мульти имеет 32-х символьный алфавит. Племя Пульти использует 64-х символьный алфавит. Вожди племён обменялись письмами. Письмо племени Мульти содержало 80 символов, а письмо племени Пульти – 70 символов. Сравните объёмы информации, содержащейся в письмах.
Ответ: 400 бит и 420 бит соответственно -
34 слайд
ЗАДАЧИ
Задача про марсиан!!!
Приветствие участникам олимпиады от марсиан записано с помощью всех символов марсианского алфавита:
ТЕВИРП!КИ!
Сколько информации оно несет?
Ответ: 30 бит. -
35 слайд
ЗАДАЧИ
ДНК человека (генетический код) можно представить себе как некоторое слово в четырёхбуквенном алфавите, где каждой буквой помечается звено цепи ДНК, или нуклеотид.
Сколько информации (в битах) содержит ДНК человека, содержащий примерно 1,5*1023 нуклеотидов?
Ответ:3*1023 бит -
36 слайд
ЗАДАЧИ на дом
1. Информационное сообщение объёмом 1,5 Кбайта содержит 3072 символа. Сколько символов содержит алфавит, при помощи которого было записано это сообщение?
2. Сообщение занимает 2 страницы и содержит 1/16 Кбайта информации. На каждой странице записано 256 символов. Какова мощность используемого алфавита?
3. Сколько килобайтов составляет сообщение, содержащее 12288 битов? -
37 слайд
РЕШЕНИЕ задачи1
Надо найти мощность алфавита N.
По условию задачи
I=1,5 Кб=1.5*1024*8=12 288 бит
I=i*k Значит, i=I/k=12 288/ 3072 = 4 бита
Так как N=2i , то N=24= 16 символов.ОТВЕТ: 16 символов
-
38 слайд
Остальные задачи попробуйте решить самостоятельно!!!
УСПЕХА!!!!
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 116 266 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 11.09.2017
- 349
- 0

Информатика ЕГЭ. Задания №1
- Учебник: «Информатика. Углубленный уровень (в 2-ух частях) », Поляков К.Ю., Еремин Е.А.
- Тема: § 9. Системы счисления
- 10.09.2017
- 1608
- 1



- 10.09.2017
- 910
- 11
- 10.09.2017
- 347
- 0
- 10.09.2017
- 362
- 1
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Информационные технологии в деятельности учителя физики»
-
Курс повышения квалификации «Организация работы по формированию медиаграмотности и повышению уровня информационных компетенций всех участников образовательного процесса»
-
Курс повышения квалификации «Развитие информационно-коммуникационных компетенций учителя в процессе внедрения ФГОС: работа в Московской электронной школе»
-
Курс повышения квалификации «Использование компьютерных технологий в процессе обучения в условиях реализации ФГОС»
-
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
-
Курс повышения квалификации «Введение в программирование на языке С (СИ)»
-
Курс профессиональной переподготовки «Управление в сфере информационных технологий в образовательной организации»
-
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Современные тенденции цифровизации образования»
-
Курс повышения квалификации «Современные языки программирования интегрированной оболочки Microsoft Visual Studio C# NET., C++. NET, VB.NET. с использованием структурного и объектно-ориентированного методов разработки корпоративных систем»