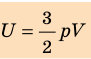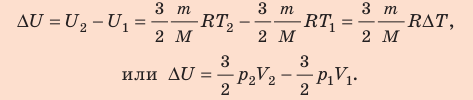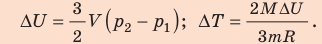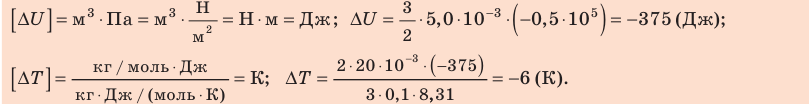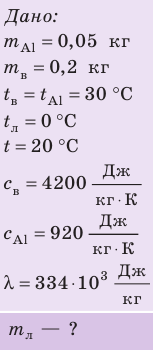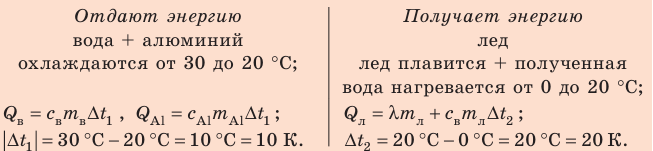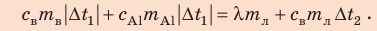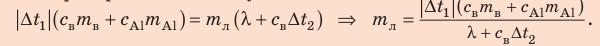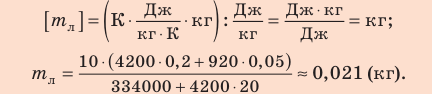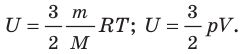Содержание:
Внутренняя энергия:
Вы знаете, что движущееся тело обладает кинетической энергией. А если оно еще и взаимодействует с другим телом, то обладает потенциальной энергией. Оба вида энергии представляют собой механическую энергию. Они взаимно превращаемы: кинетическая энергия может переходить в потенциальную и наоборот. Кроме того, вы знаете, что любое тело имеет дискретную структуру, т. е. состоит из частиц (атомов, молекул). Частицы находятся в непрерывном хаотическом движении. А частицы жидкости и твердого тела еще и взаимодействуют между собой. Следовательно, частицы обладают кинетической, а частицы жидкости и твердых тел — еще и потенциальной энергией. Сумма кинетической и потенциальной энергий всех частиц тела называется внутренней энергией. Внутренняя энергия измеряется в джоулях. Чем отличается внутренняя энергия от механической? В чем ее особенности? Может ли механическая энергия переходить во внутреннюю?
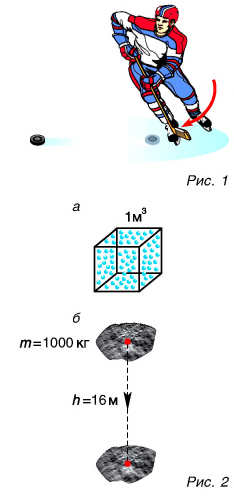
Для ответа на эти вопросы рассмотрим пример. Шайба, двигавшаяся горизонтально по льду (рис. 1), остановилась. Как изменилась ее механическая энергия относительно льда?
Кинетическая энергия шайбы уменьшилась до нуля. Положение шайбы над уровнем льда не изменилось, шайба не деформировалась. Значит, изменение потенциальной энергии равно нулю. Означает ли это, что се механическая (кинетическая) энергия исчезла бесследно? Нет. Механическая энергия шайбы перешла во внутреннюю энергию шайбы и льда.
А может ли внутренняя энергия тела, как механическая, быть равной нулю? Движение частиц, из которых состоит тело, не прекращается даже при самых низких температурах. Значит, тело всегда (подчеркиваем, всегда) обладает некоторым запасом внутренней энергии. Его можно либо увеличить, либо уменьшить — и только!
Велико ли значение внутренней энергии тела? Энергия одной частицы, например кинетическая, в силу незначительности ее массы чрезвычайно мала. Расчеты для средней энергии поступательного движения молекулы кислорода показывают, что ее значение при комнатной температуре
Главные выводы:
- Независимо от того, есть у тела механическая энергия или нет, оно обладает внутренней энергией.
- Внутренняя энергия тела равна сумме кинетической и потенциальной энергий частиц, из которых оно состоит.
- Внутренняя энергия тела всегда не равна нулю.
Способы изменения внутренней энергии
Чтобы изменить механическую энергию тела, надо изменить скорость его движения, взаимодействие с другими телами или взаимодействие частей тела. Вы уже знаете, что это достигается совершением работы.
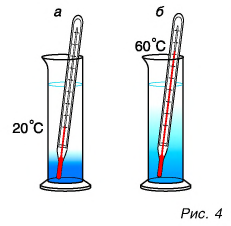
Как можно изменить (увеличить или уменьшить) внутреннюю энергию тела? Рассуждаем логически. Внутренняя энергия определяется как сумма кинетической и потенциальной энергий частиц. Значит, нужно изменить либо скорость движения частиц, либо их взаимодействие (изменить расстояния между ними). Очевидно, можно изменить и скорость, и расстояния между частицами одновременно. Изменить скорость частиц тела можно, увеличив или уменьшив его температуру. Действительно, наблюдения за диффузией показывают, что быстрота ее протекания увеличивается при нагревании (рис. 4, а, б).
Значит, увеличивается средняя скорость движения частиц, а следовательно, их средняя кинетическая энергия. Отсюда следует важный вывод: температура является мерой средней кинетической энергии частиц.
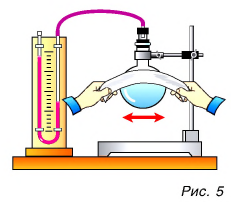
Как изменить кинетическую энергию частиц тела? Существуют два способа. Рассмотрим их на опытах. Будем натирать колбу с воздухом полоской сукна (рис. 5).
Через некоторое время уровень жидкости в правом колене манометра (см. рис. 5) опустится, т. е. давление воздуха в колбе увеличится. Это говорит о нагревании воздуха. Значит, увеличилась скорость движения и кинетическая энергия его молекул, а следовательно, и внутренняя энергия. Но за счет чего? Очевидно, за счет совершения механической работы при трении сукна о колбу. Нагрелась колба, а от нее — газ.
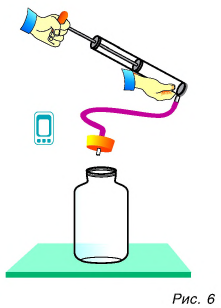
Проведем еще один опыт. В толстостенный стеклянный сосуд нальем немного воды (чайную ложку для увлажнения воздуха в нем. Насосом (рис. 6) будем накачивать в сосуд воздух. Через несколько качков пробка вылетит, а в сосуде образуется туман. Из наблюдений за окружающей средой мы знаем, что туман появляется тогда, когда после теплого дня наступает холодная ночь. Образование тумана в сосуде свидетельствует об охлаждении воздуха, т. е. об уменьшении его внутренней энергии. Но почему уменьшилась энергия? Потому что за ее счет совершена работа по выталкиванию пробки из сосуда.
Сравним результаты опытов. В обоих случаях изменилась внутренняя энергия газа, но в первом опыте она увеличилась, так как работа совершалась внешней силой (над колбой с газом), а во втором — уменьшилась, ибо работу совершала сила давления самого газа.
А можно ли, совершая работу, изменить потенциальную энергию взаимодействия молекул?
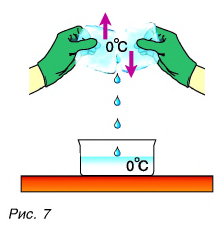
Опять обратимся к опыту. Два куска льда при О °C будем тереть друг о друга (рис. 7).
Лед превращается в воду, при этом температура воды и льда остается постоянной, равной О °C (см. рис. 7). На что тратится механическая работа силы трения?
Конечно же, на изменение внутренней энергии!
Но кинетическая энергия молекул не изменилась, так как температура не изменилась. Лед превратился в воду. При этом изменились силы взаимодействия молекул 
Совершение механической работы — один из способов изменения внутренней энергии тела.
А есть ли возможность изменить внутреннюю энергию тела, не совершая механическую работу?
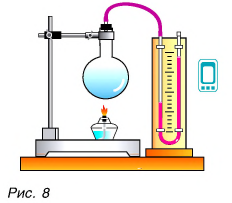
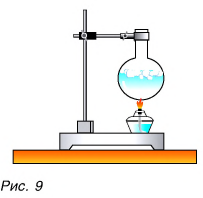
Да, есть. Нагреть воздух в колбе (рис. 8), расплавить лед (рис. 9) можно с помощью спиртовки, передав и воздуху, и льду теплоту. В обоих случаях внутренняя энергия увеличивается.
При охлаждении тел (если колбы со льдом и воздухом поместить в морозильник) их внутренняя энергия уменьшается. Теплота от тел передается окружающей среде.
Процесс изменения внутренней энергии тела, происходящий без совершения работы, называется теплопередачей (теплообменом).
Таким образом, совершение механической работы и теплопередача — два способа изменения внутренней энергии тела.
Величину, равную изменению внутренней энергии при теплопередаче, называют количеством теплоты (обозначается Q). Единицей количества теплоты, как работы и энергии, в СИ является 1 джоуль.
Для любознательных:
Физики XVIII в. и первой половины XIX в. рассматривали теплоту не как изменение энергии, а как особое вещество — теплород — жидкость (флюид), которая может перетекать от одного тела к другому. Если тело нагревалось, то считалось, что в него вливался теплород, а если охлаждалось — то выливался. При нагревании тела расширяются. Это объяснялось тем, что теплород имеет объем. Но если теплород — вещество, то тела при нагревании должны увеличивать свою массу. Однако взвешивания показывали, что масса тела не менялась. Поэтому теплород считали невесомым. Теорию теплорода поддерживали многие ученые, в том числе и такой гениальный ученый, как Г. Галилей. Позже Дж. Джоуль на основании проведенных им опытов пришел к выводу, что теплород не существует и что теплота есть мера изменения кинетической и потенциальной энергий движущихся частиц тела.
В дальнейшем выражение «сообщить телу количество теплоты» мы будем понимать как «изменить внутреннюю энергию тела без совершения механической работы, т. е. путем теплообмена». А выражение «нагреть тело» будем понимать как «повысить его температуру» любым из двух способов.
Главные выводы:
- Внутреннюю энергию тела можно изменить путем совершения механической работы или теплопередачи (теплообмена).
- Изменение внутренней энергии при нагревании или охлаждении тела при постоянном объеме связано с изменением средней кинетической энергии его частиц.
- Изменение внутренней энергии тела при неизменной температуре связано с изменением потенциальной энергии его частиц.
Основы термодинамики
МКТ стала общепризнанной на рубеже XIX и XX веков. Задолго до ее создания исследованием тепловых процессов занималась термодинамика — раздел физики, изучающий превращение внутренней (тепловой) энергии в другие виды энергии и наоборот, а также количественные соотношения при таких превращениях.
- Заказать решение задач по физике
Внутренняя энергия и ее особенности
Внутренняя энергия макроскопического тела определяется характером движения и взаимодействия всех микрочастиц, из которых состоит тело (система тел). Таким образом, к внутренней энергии следует отнести:
- кинетическую энергию хаотического (теплового) движения частиц вещества (атомов, молекул, ионов);
- потенциальную энергию взаимодействия частиц вещества;
- энергию взаимодействия атомов в молекулах (химическую энергию);
- энергию взаимодействия электронов и ядра в атоме и энергию взаимодействия нуклонов в ядре (внутриатомную и внутриядерную энергии).
Однако для описания тепловых процессов важно не столько значение внутренней энергии, как ее изменение. При тепловых процессах химическая, внутриатомная и внутриядерная энергии практически не изменяются. Именно поэтому внутренняя энергия в термодинамике определяется как сумма кинетических энергий хаотического (теплового) движения частиц вещества (атомов, молекул, ионов), из которых состоит тело, и потенциальных энергий их взаимодействия.
Внутреннюю энергию обозначают символом U.
Единица внутренней энергии в СИ — джоуль: [U]=1 Дж (J).
Особенности внутренней энергии идеального газа
- Атомы и молекулы идеального газа практически не взаимодействуют друг с другом, поэтому внутренняя энергия идеального газа равна кинетической энергии поступательного и вращательного движений его частиц.
- Внутренняя энергия данной массы идеального газа прямо пропорциональна его абсолютной температуре. Докажем данное утверждение для одноатомного газа. Атомы такого газа движутся только поступательно, поэтому, чтобы определить его внутреннюю энергию, следует среднюю кинетическую энергию поступательного движения атомов умножить на количество атомов:
Итак, для одноатомного идеального газа:
. Используя уравнение состояния
, выражение для внутренней энергии идеального одноатомного газа можно представить так:
- Внутренняя энергия — функция состояния системы, то есть она однозначно определяется основными макроскопическими параметрами (p, V, T), характеризующими систему. Независимо от того, каким образом система переведена из одного состояния в другое, изменение внутренней энергии будет одинаковым.
- Внутреннюю энергию можно изменить двумя способами: совершением работы и теплопередачей.
Какие существуют виды теплопередачи
Теплопередача (теплообмен) — процесс изменения внутренней энергии тела или частей тела без совершения работы. Процесс теплопередачи возможен только при наличии разности температур. Самопроизвольно тепло всегда передается от более нагретого тела к менее нагретому. Чем больше разность температур, тем быстрее — при прочих равных условиях — протекает процесс передачи тепла.
| Виды теплопередачи | ||
|---|---|---|
| Теплопроводность | Конвекция | Излучение |
|
Вид теплопередачи, который обусловлен хаотическим движением частиц вещества и не сопровождается переносом этого вещества. Лучшие проводники тепла — металлы, плохо проводят тепло дерево, стекло, кожа, жидкости (за исключением жидких металлов); самые плохие проводники тепла — газы. Передача энергии от горячей воды к батарее отопления, от поверхности воды до ее нижних слоев и т. д. происходит благодаря теплопроводности. |
Вид теплопередачи, при котором тепло переносится потоками жидкости или газа. Теплые потоки жидкости или газа имеют меньшую плотность, поэтому под действием архимедовой силы поднимаются, а холодные потоки — опускаются. Благодаря конвекции происходит циркуляция воздуха в помещении, нагревается жидкость в стоящей на плите кастрюле, существуют ветры и морские течения и т. д. В твердых телах конвекция невозможна. | Вид теплопередачи, при котором энергия передается посредством электромагнитных волн. Излучение — универсальный вид теплопередачи: тела всегда излучают и поглощают инфракрасное (тепловое) излучение. Это единственный вид теплообмена, возможный в вакууме (энергия от Солнца передается только излучением). Лучше излучают и поглощают энергию тела с темной поверхностью. |
Как определить количество теплоты
Количество теплоты Q — это физическая величина, равная энергии, которую тело получает (или отдает) в ходе теплопередачи.
Единица количества теплоты в СИ — джоуль: [П] =1 Дж (J).
Из курса физики 8 класса вы знаете, что количество теплоты, которое поглощается при нагревании вещества (или выделяется при его охлаждении), вычисляют по формуле: Q=cm∆Т=cm∆t , где c — удельная теплоемкость вещества; m — масса вещества; 
Обратите внимание! Произведение удельной теплоемкости на массу вещества, из которого изготовлено тело, называют теплоемкостью тела: C=cm . Если известна теплоемкость C тела, то количество теплоты, которое получает тело при изменении температуры на ∆T, вычисляют по формуле: Q=C∆T .
| Расчет количества теплоты при фазовых переходах | |
|---|---|
| Кристаллическое состояние ↔ Жидкое состояние | Жидкое состояние ↔ Газообразное состояние |
|
Температуру, при которой происходят фазовые переходы «кристалл → жидкость» и «жидкость → кристалл», называют температурой плавления. Температура плавления зависит от рода вещества и внешнего давления. Количество теплоты Q, которое поглощается при плавлении кристаллического вещества (или выделяется при кристаллизации жидкости), вычисляют по формуле: Q = λm, где m — масса вещества; λ — удельная теплота плавления. |
Фазовые переходы «жидкость → пар» и «пар → жидкость» происходят при любой температуре. Количество теплоты Q, которая поглощается при парообразовании (или выделяется при конденсации), вычисляют по формуле: Q=rm (Q=Lm), где m — масса вещества; r (L) — удельная теплота парообразования при данной температуре (обычно в таблицах представлена удельная теплота парообразования при температуре кипения жидкости). |
| Напомним: и при плавлении, и при кипении температура вещества не изменяется. |
Пример решения задачи №1
Неон массой 100 г находится в колбе объемом 5,0 л. В процессе изохорного охлаждения давление неона уменьшилось с 100 до 50 кПа. На сколько при этом изменились внутренняя энергия и температура неона?
Решение:
Неон — одноатомный газ; для таких газов изменение внутренней энергии равно:
Поскольку охлаждение изохорное, объем неона не изменяется: 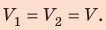
Проверим единицы, найдем значения искомых величин:
Анализ результатов. Знак «–» свидетельствует о том, что внутренняя энергия и температура неона уменьшились, — это соответствует изохорному охлаждению. Ответ: ∆U = –375 Дж; ∆T = –6 К.
Пример решения задачи №2
Внутренний алюминиевый сосуд калориметра имеет массу 50 г и содержит 200 г воды при температуре 30 °С. В сосуд бросили кубики льда при температуре 0 °С, в результате чего температура воды в калориметре снизилась до 20 °С. Определите массу льда. Удельные теплоемкости воды и алюминия: 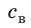
Анализ физической проблемы.
Калориметр имеет такое устройство, что теплообмен с окружающей средой практически отсутствует, поэтому для решения задачи воспользуемся уравнением теплового баланса. В теплообмене участвуют три тела: вода, внутренний сосуд калориметра, лед.
Решение:
Запишем уравнение теплового баланса:
После преобразований получим:
Проверим единицу, найдем значение искомой величины:
Ответ: 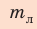
Выводы:
- В термодинамике под внутренней энергией U тела понимают сумму кинетических энергий хаотического движения частиц вещества, из которых состоит тело, и потенциальных энергий их взаимодействия. Внутренняя энергия однозначно определяется основными макроскопическими параметрами (p, V, T), характеризующими термодинамическую систему. Внутреннюю энергию идеального одноатомного газа определяют по формулам:
- Внутреннюю энергию можно изменить двумя способами: совершением работы и теплопередачей. Существует три вида теплопередачи: теплопроводность, конвекция, излучение.
- Физическую величину, равную энергии, которую тело получает или отдает при теплопередаче, называют количеством теплоты (Q): Q=cm∆T = С∆T — количество теплоты, которое поглощается при нагревании тела (или выделяется при его охлаждении); Q = λm — количество теплоты, которое поглощается при плавлении вещества (или выделяется при кристаллизации); Q=rm (Q=Lm) — количество теплоты, которое поглощается при парообразовании вещества (или выделяется при конденсации).
- Теплопроводность в физике
- Конвекция в физике
- Излучение тепла в физике
- Виды излучений в физике
- Машины и механизмы в физике
- Коэффициент полезного действия (КПД) механизмов
- Тепловые явления в физике
- Тепловое движение в физике и его измерение
Сегодня мы поговорим о
понятии энергии в механике. То есть мы будем рассматривать только механические
процессы, без оглядки на тепловые или электромагнитные явления.
Рассмотрим простые примеры:
мы можем растягивать или сжимать пружину, то есть её длина будет увеличиваться
или уменьшаться. При этом пружина будет стремиться воспрепятствовать
деформации. Точно также, можно раскачать маятник, и при этом, его скорость и
положение будут постоянно меняться.
При этих действиях, мы
сами совершаем работу или, как мы говорим, затрачиваем энергию. Можно привести
ещё много подобных примеров, но все они приведут к одному и тому же выводу: совершение
работы не проходит для системы тел бесследно. Таким образом, энергия характеризует
способность тела совершить работу.
Иными словами, совершение
работы над телом приводит к изменению его состояния.
В механике состояние
системы определяется положением тел и их скоростями.
Давайте рассмотрим простой пример движения автомобиля по прямому участку
дороги. Допустим, этот автомобиль движется с постоянным ускорением вдоль оси х.
Как мы помним, полная работа равна работе равнодействующей силы. Таким образом,
работа, совершаемая в процессе движения автомобиля равна произведению массы, ускорения
и перемещения:
В одном из предыдущих
уроков мы вывели формулу, связывающую перемещение, скорость и ускорение.
Используя эту формулу, мы можем преобразовать выражение для работы. Вы уже
знаете, что кинетическая энергия равна половине произведения массы тела и квадрата
его скорости. Поэтому, можно заключить, что работа силы, действующей на тело
в течение некоторого времени, равна изменению кинетической энергии за это же
время.
Мы сделали этот вывод,
основываясь на прямолинейном движении. Но, используя более сложные
математические операции можно доказать, что эта формула справедлива для
любого движения, независимо от траектории.
Нетрудно догадаться, что
энергия, как и работа, измеряется в джоулях: [𝐸]=[Дж].
В этом можно легко убедиться, сделав проверку размерности. Рассмотрим формулу
для кинетической энергии:
Примеры решения задач.
Задача 1. Мяч
массой 0,5 кг скатывается с одного холмика и закатывается на другой.
Определите, какая работа была совершена внешними силами, если изначально мяч
обладал скоростью 4 м/с, а на втором холмике стал обладать скоростью, равной 2
м/с.
Сразу хотелось бы
обратить внимание, что через силы эту задачу решить было бы крайне сложно. Ведь
мяч катится по криволинейной траектории, из-за чего вектор перемещения
постоянно меняется, да и силы не остаются постоянными. Используя же формулу,
которую мы выучили на сегодняшнем уроке, задача существенно упрощается.
Из решения этой простой
задачи можно сделать важный вывод: энергия тела не зависит от того, каким
образом тело пришло в то или иное состояние. Имеет значение только то, в каком
состоянии тело находится в данный момент времени.
Действительно, ведь для
решения задачи мы лишь сравнили начальное и конечное состояние тела, совершенно
не заботясь о том, что с ним происходило в процессе изменения состояния.
Задача 2. Автомобиль
массой 900 кг останавливается под действием силы трения. Известно, что к
моменту полной остановки работа силы трения составила –2,5 кДж. Найдите начальную скорость автомобиля.
Содержание:
- Теоремы про изменение кинетической энергии материальной точки и системы
- Кинетическая энергия материальной точки и системы материальных точек. Теорема Кенига
- Кинетическая энергия твердого тела. Соотношение между основными динамическими величинами
- Представление проекций количества движения и механического момента через кинетическую энергию
- Расчет кинетической энергии для отдельных случаев движения твердого тела
- Теорема об изменении кинетической энергии материальной точки
- Работа силы, приложенной к материальной точке. Теорема о работе
- Теорема (о работе равнодействующей)
- Теорема (о работе сил на последовательных перемещениях)
- Работа, выполняемая силой тяжести
- Работа, выполняемая центральной силой
- Работа, выполняемая силой упругости
- Работа внешних сил, приложенных к твердому телу
- Теорема об изменении кинетической энергии системы материальных точек
Согласно теореме об изменении кинетической энергии работа равна разности конечной и начальной кинетических энергий, при этом начальная кинетическая энергия равна 0, поскольку начальная скорость равна 0, и тогда: Следовательно, кинетическая энергия тела массой , движущегося со скоростью , равна работе, которую нужно совершить, чтобы сообщить телу эту скорость.
Изменение кинетической энергии системы равно работе всех внутренних и внешних сил, действующих на тела системы. Теорема допускает обобщение на случай неинерциальных систем отсчёта. В этом случае к работе всех внешних и внутренних сил необходимо добавить работу переносных сил инерции (кориолисовы силы инерции не могут производить работу).
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Теоремы про изменение кинетической энергии материальной точки и системы
Энергией называют физическую величину, которая является скалярной мерой движения материи при переходе одной формы движения в другую, например механической в тепловую и тому подобное. Итак, энергия характеризует различные формы движения материи, в том числе и механическое движение. Полная механическая энергия Е равна сумме кинетической Т и потенциальной П энергий:

Как отмечалось в п. 16.2, кинетическая энергия Т является второй мерой механического движения. Эта мера, введенная и названа Г. Лейбницем «живой силой», была обозначена им через 

Кинетическая энергия материальной точки и системы материальных точек. Теорема Кенига
Кинетической энергией называют скалярную меру механического движения в неподвижной системе координат, которая равна половине произведения массы точки на квадрат ее скорости, то есть

В зависимости от способа задания движения точки выражение для кинетической энергии будет разным.
1. Если движение материальной точки задано в векторной форме 
точки 

2. Если движение точки задано в координатной форме 


3. Если движение точки задано в натуральной форме, то кинетическая энергия

где 
Кинетической энергией системы материальных точек называют сумму кинетических
энергий всех точек, входящих в систему:

Из приведенных формул видно, что кинетическая энергия является положительной величиной. При этом скорости 
В основном движение материальной системы относительно инерциальных осей 
рис. 16.5) целесообразно представить как сложный и разложить его на простые движения для упрощения вычисления кинетической энергии системы.
Введем подвижную систему координат 
Будем рассматривать движение материальной системы как относительно неподвижной системы координат 

Пусть 

радиус-вектор начала подвижной системы координат 



где 

движущейся поступательно. Подставив выражение (17.7) для скорости 


В этом выражении 





где 
Итак, кинетическая энергия материальной системы в ее абсолютном движении имеет три составляющие: кинетическую энергию 




В частном случае, когда начало подвижной системы координат О совпадает с центром масс (инерции) С системы, то 

Последнее уравнение позволяет сформулировать теорему Кенига: кинетическая энергия
системы материальных точек равна сумме кинетической энергии поступательного (переносного) движения системы вместе с центром масс и кинетической энергии движения системы относительно центра масс.
В следующем параграфе рассмотрим, как использовать полученные формулы для определения кинетической энергии в конкретной случаях.
Кинетическая энергия твердого тела. Соотношение между основными динамическими величинами
Рассмотрим случай, когда система материальных точек неизменна, то есть твердые телом. Введем в дополнение к уже введенных в п. 17.1 еще одну систему координат
(см. рис. 16.5), которая неизменно связана с твердым телом и вращается вместе с ним вокруг точки О с угловой скоростью 

примет вид:

Используя выражение для 


Здесь

где индекс 
Касаемо твердого тела теорему Кенинга (Точка О совпадает с центром масс, 

и сформулировать так: кинетическая энергия твердого тела равна сумме кинетической
энергии его поступательного (переносного) движения вместе с центром масс и кинетической энергии вращательного движения тела вокруг центра масс.
Несмотря на то, что формула для вычисления кинетической энергии твердого тела
проще тогда, когда полюс О совпадает с центром масс, в практических задачах, возникающих при исследовании роботов-манипуляторов, гироскопических приборов, движущихся объектов (кораблей, самолетов, ракет, подводных лодок и т.п.), полюс целесообразно выбирать не в центре масс системы. В связи с этим формулы (17.9) и (17.12) имеют большое практическое значения. Рассмотрим, как можно вывести выражение для количества движения Q и кинетического момента 
Соотношение между основными динамическими величинами 

то есть сумма скалярного произведения количества движения системы на скорость полюса 

Тогда

где
Если учесть, что 


Рассмотрим подробнее последний скалярное произведение с учетом выражения для

Поскольку 



или

Подставляя (17.19) в выражение (17.17) и сравнивая его с (17.12), получим:

что и требовалось доказать. Отметим, что скалярное произведение 

то есть является динамическим инвариантом. Действительно, по формуле (16.48)

Умножив обе части последней равенства скалярно на 
получим выражение (17.21). Соотношение (17.15) дает возможность охарактеризовать механическое движение твердого тела. Действительно, две меры механического движения: количество движения и кинетическая энергия в свете диалектического материализма с основными мерами механического движения системы материальных точек. Как видно из формулы (17.15), количество движения Q и кинетический момент 
Представление проекций количества движения и механического момента через кинетическую энергию
Поскольку кинетическая энергия является однородной функцией скорости со степенью однородности, равной 2, то, воспользовавшись формулой Эйлера для однородных функций, можем записать:

Кроме того, раскрывая скалярные произведения в соотношении (17.15), получим:

Сравнивая правые части (17.23) и (17.24), найдем искомые соотношения:


С равенства (17.19) для частного случая вращательного движения тела относительно полюса
получим следующие соотношения:

Понятно, что приведенные соотношения (17.25) — (17.27) справедливы также тогда, когда спроектировать 
Расчет кинетической энергии для отдельных случаев движения твердого тела
Кинетическая энергия твердого тела, которое движется поступательно. При поступательном движении твердого тела 
Для этого движения из выражения (17.12) получим

Итак, кинетическая энергия твердого тела, движущегося поступательно, равна половине произведения массы тела на квадрат его скорости.
Кинетическая энергия твердого тела, которое вращается вокруг неподвижной точки. При вращении тела вокруг неподвижной точки О (см. рис. 16.5) 

Учитывая, что проекции кинетического момента 
получим:

Подставим соотношение (17.30) в (17.29), тогда

Если оси координат 



Выражение для кинетической энергии не изменится, если записать проекции угловой скорости на неподвижные оси 

Предлагаем самостоятельно вывести формулу (17.31) по-другому, исходя из того, что
вращения твердого тела вокруг неподвижной точки можно считать вращением вокруг мгновенной оси. Тогда:

В этом случае следует воспользоваться формулой (15.69) для момента инерции относительно произвольной оси и учесть, что
Кинетическая энергия твердого тела при вращении его вокруг неподвижной оси. Пусть твердое тело вращается вокруг неподвижной оси, например 
и из выражения (17.31) получим:

Кинетическая энергия твердого тела при плоском движении. При этом движении тела вектор угловой скорости 



В частном случае, когда полюс О размещается в центре масс, это выражение упрощается:

Кинетическая энергия твердого тела при пространственном движении. В этом случае применяют общую формулу (17.12), которая в развернутом виде принимает вид:

Пример 1. Планетарный механизм (рис. 17.1) размещен в горизонтальной плоскости и приводится в движение водилом 




Решение. Для определения кинетической энергии всей системы, то есть данного механизма сначала установим характер движения каждого звена. Первое колесо неподвижно, водило вращается с угловой скоростью 
или

поскольку колесо I недвижимое, то 

Составим пропорции, учитывая зацеплении колес:


С первой пропорции имеем: 

Итак, колесо III осуществляет мгновенно-поступательное движение. Скорости всех его точек одинаковы и равны скорости точки В, поэтому
Учитывая, что 
Далее, по теореме Кенига, вычислим кинетическую энергию колеса II:

Тут 


Вычислим кинетическую энергию водила ОВ, учитывая, что 



Пример 2. Тонкий диск массой m и радиусом г катится по горизонтальной плоскости (рис. 17.2) так, что скорость центра масс равна 
Решение. 1. По теореме Кенига кинетическая энергия тела равна сумме кинетической энергии поступательного движения вместе с центром масс и кинетической энергии движения тела относительно центра масс, которое является вращательным, то есть:
В данном случае 
2. Диск выполняет мгновенное вращательное движение относительно оси, проходящей через мгновенный центр скоростей, поэтому
Угловая скорость равна
По теореме И. Гюйгенса — Штейнера имеем:
Подставив значение момента инерции 

что совпадает с предыдущим результатом.
Пример 3. Подводная лодка массой m изображена в форме модели физического маятника, в котором центр масс смещен вниз по вертикали (оси 






Найти выражения для кинетической энергии лодки и выразить через нее количество движения и момент количества движения лодки в проекциях на оси
Решение. Кинетическую энергию вычислим по формуле (17.35) с учетом
Учитывая, что 
Используя теперь соотношение (17.25) и (17.26), получим
Теорема об изменении кинетической энергии материальной точки
Теорема. Прирост кинетической энергии материальной точки на некотором отрезке дуги ее траектории равен работе силы, приложенной к точке, на этом самом отрезке дуги траектории.
Доказательство. Пусть на материальную точку М действует сила 




Чтобы в это уравнение вошла кинетическая энергия 


Отсюда легко получить

Поскольку 

Слева в равенстве (17.41) записан элементарный прирост кинетической энергии, а справа —
физическая величина, которая называется элементарной работой и обозначается 

Итак, элементарная работа равна скалярному произведению силы на элементарное перемещение, вызванное этой силой. Элементарная работа не всегда будет полным дифференциалом некоторой скалярной функции координат точки. Подставляя 
(17.41), получим:

Это равенство выражает теорему об изменении кинетической энергии материальной точки в дифференциальной форме: дифференциал кинетической энергии материальной точки равен элементарной работе сил, действующих на точку.
Интегрируя обе части (17.43), получим:

или

Теорема доказана.
Через 
В выражении (17.45) через А обозначена работа силы на конечном отрезке траектории, которая определяется формулой:

Как видно из доказанной теоремы, изменение кинетической энергии (второй степени механического движения) дает новую физическую величину, которая называется работой. Чтобы иметь возможность применить теорему об изменении кинетической энергии к решению задач, надо изучить основные свойства работы.
Работа силы, приложенной к материальной точке. Теорема о работе
Понятие работы силы возникло в связи с изменением второй степени механического движения (кинетической энергии). Элементарная работа силы является скалярной степенью воздействия силы, и равна скалярному произведения (17.42) силы на элементарное перемещение точки ее приложения. В случае натурального способа задания движения 

Полная работа при этом будет определяться криволинейным интегралом:

где 


От криволинейного интеграла (17.49) можно перейти к определенному интегралу, если
учесть, что 

где 



Наряду с понятием работы вводят также понятие мощности:

Очевидно, что мощность нельзя рассматривать как производную от работы, взятую по времени, поскольку 
Мощность N — это физическая величина, характеризующая скорость выполнения работы силой, которая приложена к материальной точке, и равна скалярному произведению силы на скорость точки. Рассмотрим некоторые элементарные теоремы о работе.
Теорема (о работе равнодействующей)
Работа равнодействующей системы сил равна алгебраической сумме работ составляющих сил.
Доказательство. Пусть на точку действует система, состоящая из 

Умножив обе части равенства скалярно на 
или

Теорема (о работе сил на последовательных перемещениях)
Элементарная работа
постоянной силы 
Доказательство теоремы формально аналогичное доказательству предыдущей теоремы.
В завершение рассмотрим основные единицы мощности и работы. За единицу мощности в 







Работа, выполняемая силой тяжести
Пусть материальная точка весом 
движется по некоторой траектории из положения 



Элементарная работа этой силы, согласно (17.49),

Знак минус означает, что сила (рис. 17.5, в) направлена в противоположную сторону направления оси Oz. Итак, работа, выполненная силой тяжести при перемещении точки М из положения 


Поскольку разность 


Как видно из формулы (17.57), работа силы тяжести материальной точки равна произведению силы тяжести Р на разность высот начального и конечного положения точки.
Отметим, что работа, выполняемая силой тяжести 
Работа, выполняемая центральной силой
Напомним, что центральной силой 
Вычислим работу А центральной силы 


Проекцию центральной силы на направление 


Где 




Однако, поскольку 

Проинтегрируем последнее выражение и получим полную работу центральной силы:

По выражению (17.62) видим, что и в случае центральной силы работа не зависит от
формы траектории материальной точки, на которую действует центральная сила, а зависит только от начального и конечного положений точки. Формула (17.62) позволяет определять работу центральной силы в отдельных случаях, например, силы всемирного тяготения, силы взаимодействия между электрическими зарядами, то есть при конкретных значениях
Работа, выполняемая силой упругости
Вычислим работу, осуществленную силой 






где с — коэффициент жесткости пружины; 





Как видно из этой формулы, работа силы упругости не зависит от формы траектории
точки М, а зависит только от крайних положений точки. В частном случае, когда траекторией точки 


где h— полное удлинение пружины. Как видно из последней формулы, работа силы упругости пружины в случае отклонения ее от недеформированного состояния пропорциональна квадрату полного удлинения пружины.
Пример 4. Две частицы заряженные положительным электричеством. Заряд первой частицы равна 100 абсолютным электростатическим единицам (СГСЭ), заряд второй частицы — в 10 раз меньше. Первая частица неподвижна, а вторая движется под действием силы отталкивания 
Определить верхнюю границу для скорости частицы, движущейся, учитывая только действие силы отталкивания 


Решение. На материальные частицы действует сила 
второй частицы от неподвижной частицы сила F на пройденном частицей расстоянии выполнит работу. При этом изменение кинетической энергии будет равно выполненной работе:

Поскольку 

Сила, действующая на материальную точку, переменная, то есть 
Итак, элементарная работа:
полная работа
Подставляя это значение в (2), получим
Работа внешних сил, приложенных к твердому телу
Пусть к точкам твердого тела (см. рис. 16.5) приложена совокупность внешних сил 


Поскольку 


Подставив (17.67) в (17.66) и учитывая, что 


где 
Переставим местами

или

Поскольку 


поворота, то окончательно выражение для элементарной работы примет вид:

Следовательно, элементарная работа внешних сил, приложенных к твердому телу, равна сумме работы главного вектора внешних сил, которая осуществляется на элементарном перемещении полюса О, и работы главного момента этих сил, вычисленной в отношении центра О, на элементарном вращательном перемещении 


для определения мощности сил, приложенных к телу, то есть мощность внешних сил, приложенных к телу, равна сумме скалярного произведения главного вектора на скорость полюса О и скалярного произведения главного момента этих сил относительно данного полюса на угловую скорость вращения тела.
В отдельных случаях, когда тело выполняет вращение вокруг неподвижной оси, например 


где 
Теорема об изменении кинетической энергии системы материальных точек
Теорема. Прирост кинетической энергии системы материальных точек через некоторый промежуток времени равен сумме работ внешних и внутренних сил, действующих на точки системы в течение рассматриваемого промежутка времени.
Доказательство. Пусть система состоит 





Исходя из определения кинетической энергии системы (17.6) и подытожив, получим:

или

где 

действуют на систему. Итак, теорема доказана.
Примечания:
1. В случае твердого тела в правой части равенства (17.75) будет сумма работ только внешних сил, поскольку внутренние силы в твердом теле уравновешиваются и их работа равна нулю.
2. Анализ, основных или общих, четырех теорем динамики системы убеждает в том, что
только теорема об изменении кинетической энергии системы содержит внутренние силы, которые влияют на изменение кинетической энергии, в отличие от трех первых теорем, когда внутренние силы не влияли на изменение количества движения, на движение центра масс и изменение кинетического момента. Следовательно, кинетическая энергия как вторая мера механического движения полнее отражает свойства этого движения системы материальных точек.
3. Все доказанные основные теоремы динамики свободной системы пригодны и для несвободной системы. Для этого надо сначала применить аксиому об освобождении от связей и реакции связей отнести к активным сил.
Чтобы подтвердить глубокие связи между основными динамическими величинами, покажем на примере твердого тела, как теорему об изменении кинетической энергии можно вывести из соотношения (17.15).
Выберем полюс в центре масс, тогда соотношение (17.15) примет вид

Продифференцируем левую и правую части этого равенства, тогда:

Согласно (16.12) и (16.16) 

Из соотношения (17.78) следует

Покажем, что аналогично (17.79) имеет место такое же соотношение для кинетического
момента:

Действительно, согласно теореме об изменении кинетического момента системы (16.70),

Тогда, умножив равенство (17.81) скалярно на 

Остается доказать, что 
Скалярное произведение 

Если оси 

Поскольку моменты инерции 

что и требовалось доказать. Подставим соотношения (17.79) и (17.80) в (17.77), тогда

Сравнивая правую часть выражения (17.86) с (17.71), легко заметить, что она равна удвоенной мощности внешних сил:

Следовательно

Умножив левую и правую части на 

Отметим, что изложена методика доказательства теоремы об изменении кинетической энергии из соотношения между основными динамическими величинами показывает беспредметность дискуссии о мерах движения, возникшей в XIX в.
Пример 5. Космический аппарат, который состоит из двух тел корпуса и маховика 









1) соотношение между углами поворота маховика и космического аппарата;
2) угловую скорость, которую нужно предоставить маховику, чтобы остановить вращение космического аппарата относительно оси
3) работу, которую нужно затратить, чтобы при помощью вращений маховика остановить вращение космического аппарата.
Решение. Начнем решение задачи с третьего вопроса.
Воспользуемся теоремой об изменении кинетической энергии системы. Кинетическая энергия системы состоит из кинетических энергий двух тел корпуса аппарата и маховика. Внешние силы в данной задачи отсутствуют, а взаимодействие маховика и аппарата
происходит под действием внутренних сил. Поэтому

Внутренние силы, которые вызывают вращения маховика 
Система состоит из двух тел, вращающихся относительно оси 




где 


В момент прекращения вращения космического аппарата 

Подставив выражения (3) и (2) в (1), получим
или

Выражение (4) дает возможность определить работу внутренних сил 


системы сохраняется постоянным, поскольку главный момент внешних сил равен нулю.
Для любого момента времени получим:
Поскольку при 

Откуда

Из выражения (6) видим, что вращение аппарата прекратится 

Подставив теперь соотношение (7) в выражение (4), найдем работу внутренних сил, которую необходимо затратить, чтобы остановить вращение аппарата.

Для того чтобы найти ответ на первый вопрос, будем считать, что аппарат повернется на угол 



получим из соотношения (6)

Выражения (9), (8), (6) и является решением задачи. Отметим, что когда 


Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Момент силы
- Пара сил
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет ферм
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Параллельные силы
- Система произвольно расположенных сил
- Сосредоточенные силы и распределенные нагрузки
- Кинематика
- Кинематика твердого тела
- Движения твердого тела
- Динамика материальной точки
- Динамика механической системы
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Сферическое движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Сложное движение точки
- Плоское движение тела
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Центр масс
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки
Энергия: что это такое
Если мы погуглим определение слова «Энергия», то скорее всего найдем что-то про формы взаимодействия материи. Это верно, но совершенно непонятно.
Поэтому давайте условимся здесь и сейчас, что энергия — это запас, который пойдет на совершение работы.
Энергия бывает разных видов: механическая, электрическая, внутренняя, гравитационная и так далее. Измеряется она в Джоулях (Дж) и чаще всего обозначается буквой E.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Механическая энергия
Механическая энергия — это энергия, связанная с движением объекта или его положением, способность совершать механическую работу.
Она представляет собой совокупность кинетической и потенциальной энергии. Кинетическая энергия — это энергия действия. Потенциальная — ожидания действия.
Представьте, что вы взяли в руки канцелярскую резинку, растянули ее и отпустили. Из растянутого положения резинка просто «полетит», как только вы ей позволите это сделать. В этом процессе в момент натяжения резинка обладает потенциальной энергией, а в момент полета — кинетической.
Еще один примерчик: лыжник скатывается с горы. В самом начале — на вершине — у него максимальная потенциальная энергия, потому что он в режиме ожидания действия (ждущий режим 😂), а внизу горы он уже явно двигается, а не ждет, когда с ним это случится — получается, внизу горы кинетическая энергия.
Кинетическая энергия
Еще разок: кинетическая энергия — это энергия действия. Величина, которая очевиднее всего характеризует действие — это скорость. Соответственно, в формуле кинетической энергии точно должна присутствовать скорость.
Кинетическая энергия
Ек — кинетическая энергия [Дж]
m — масса тела [кг]
v — скорость [м/с]
Чем быстрее движется тело, тем больше его кинетическая энергия. И наоборот — чем медленнее, тем меньше кинетическая энергия.
Задачка раз
Определить кинетическую энергию собаченьки массой 10 кг, если она бежала за мячом с постоянной скоростью 2 м/с.
Решение:
Формула кинетической энергии
Подставляем значения
Дж
Ответ: кинетическая энергия пёсы равна 20 Дж.
Задачка два
Найти скорость бегущего по опушке гнома, если его масса равна 20 кг, а его кинетическая энергия — 40 Дж
Решение:
Формула кинетической энергии
Выразим скорость:
Подставляем значения
Ответ: гном бежал со скоростью 2 м/с.
Онлайн-уроки физики в Skysmart не менее увлекательны, чем наши статьи!
Потенциальная энергия
В отличие от кинетической энергии, потенциальная чаще всего тем меньше, чем скорость больше. Потенциальная энергия — это энергия ожидания действия.
Например, потенциальная энергия у сжатой пружины будет очень велика, потому что такая конструкция может привести к действию, а следовательно — к увеличению кинетической энергии. То же самое происходит, если тело поднять на высоту. Чем выше мы поднимаем тело, тем больше его потенциальная энергия.
Потенциальная энергия деформированной пружины
Еп — потенциальная энергия [Дж]
k — жесткость [Н/м]
x — удлинение пружины [м]
Потенциальная энергия в поле тяжести
Еп = mgh
Еп — потенциальная энергия [Дж]
m — масса тела [кг]
g — ускорение свободного падения [м/с2]
h — высота [м]
На планете Земля g ≃ 9,8 м/с2
Задачка раз
Найти потенциальную энергию рака массой 0,1 кг, который свистит на горе высотой 2500 метров. Ускорение свободного падения считать равным 9,8 м/с2.
Решение:
Формула потенциальной энергии Еп = mgh
Подставляем значения
Eп = 0,1 · 9,8 · 2500 = 2450 Дж
Ответ: потенциальная энергия рака, свистящего на горе, равна 2450 Дж.
Задачка два
Найти высоту горки, с которой собирается скатиться лыжник массой 65 кг, если его потенциальная энергия равна 637 кДж. Ускорение свободного падения считать равным 9,8 м/с2.
Решение:
Формула потенциальной энергии Еп = mgh
Выразим высоту:
Переведем 637 кДж в Джоули.
637 кДж = 637000 Дж
Подставляем значения
м
Ответ: высота горы равна 1000 метров.
Задачка три
Два шара разной массы подняты на разную высоту относительно поверхности стола (см. рисунок). Сравните значения потенциальной энергии шаров E1 и E2. Считать, что потенциальная энергия отсчитывается от уровня крышки стола.
Решение:
Потенциальная энергия вычисляется по формуле: E = mgh
По условию задачи
m1 = m
h1 = 2h
m2 = 2m
h2 = h
Таким образом, получим, что
E1 = mg2h = 2mgh,
а E2 = 2mgh,
то есть E1 = E2.
Ответ: E1 = E2.
Закон сохранения энергии
В физике и правда ничего не исчезает бесследно. Чтобы это как-то выразить, используют законы сохранения. В случае с энергией — Закон сохранения энергии.
Закон сохранения энергии
Полная механическая энергия замкнутой системы остается постоянной.
Полная механическая энергия — это сумма кинетической и потенциальной энергий. Математически этот закон описывается так:
Закон сохранения энергии
Еполн. мех. = Еп + Eк = const
Еполн. мех. — полная механическая энергия системы [Дж]
Еп — потенциальная энергия [Дж]
Ек — кинетическая энергия [Дж]
const — постоянная величина
Задачка раз
Мяч бросают вертикально вверх с поверхности Земли. Сопротивление воздуха пренебрежимо мало. Как изменится высота подъёма мяча при увеличении начальной скорости мяча в 2 раза?
Решение:
Должен выполняться закон сохранения энергии:
В начальный момент времени высота равна нулю, значит Еп = 0. В этот же момент времени Ек максимальна.
В конечный момент времени все наоборот — кинетическая энергия равна нулю, так как мяч уже не может лететь выше, а вот потенциальная максимальна, так как мяч докинули до максимальной высоты.
Это можно описать соотношением:
Еп1 + Ек1 = Еп2 + Ек2
0 + Ек1 = Еп2 + 0
Ек1 = Еп2
Разделим на массу левую и правую часть
Из соотношения видно, что высота прямо пропорциональна квадрату начальной скорости, значит при увеличении начальной скорости мяча в два раза, высота должна увеличиться в 4 раза.
Ответ: высота увеличится в 4 раза
Задачка два
Тело массой m, брошенное с поверхности земли вертикально вверх с начальной скоростью v0, поднялось на максимальную высоту h0. Сопротивление воздуха пренебрежимо мало. Чему будет равна полная механическая энергия тела на некоторой промежуточной высоте h?
Решение
По закону сохранения энергии полная механическая энергия изолированной системы остаётся постоянной. В максимальной точке подъёма скорость тела равна нулю, а значит, оно будет обладать исключительно потенциальной энергией Емех = Еп = mgh0.
Таким образом, на некоторой промежуточной высоте h, тело будет обладать и кинетической и потенциальной энергией, но их сумма будет иметь значение Емех = mgh0.
Ответ: Емех = mgh0.
Задачка три
Мяч массой 100 г бросили вертикально вверх с поверхности земли с начальной скоростью 6 м/с. На какой высоте относительно земли мяч имел скорость 2 м/с? Сопротивлением воздуха пренебречь.
Решение:
Переведем массу из граммов в килограммы:
m = 100 г = 0,1 кг
У поверхности земли полная механическая энергия мяча равна его кинетической энергии:
Дж
На высоте h потенциальная энергия мяча есть разность полной механической энергии и кинетической энергии:
Дж
м
Ответ: мяч имел скорость 2 м/с на высоте 1,6 м
Переход механической энергии во внутреннюю
Внутренняя энергия — это сумма кинетической энергии хаотичного теплового движения молекул и потенциальной энергии их взаимодействия. То есть та энергия, которая запасена у тела за счет его собственных параметров.
Часто механическая энергия переходит во внутреннюю. Происходит этот процесс путем совершения механической работы над телом. Например, если сгибать и разгибать проволоку — она будет нагреваться.
Или если кинуть мяч в стену, часть энергии при ударе перейдет во внутреннюю.
Задачка
Какая часть начальной кинетической энергии мяча при ударе о стену перейдет во внутреннюю, если полная механическая энергия вначале в два раза больше, чем в конце?
Решение:
В самом начале у мяча есть только кинетическая энергия, то есть Емех = Ек.
В конце механическая энергия равна половине начальной, то есть Емех/2 = Ек/2
Часть энергии уходит во внутреннюю, значит Еполн = Емех/2 + Евнутр
Емех = Емех/2 + Евнутр
Емех/2 = Евнутр
Евнутр = Ек/2
Ответ: во внутреннюю перейдет половина начальной кинетической энергии
Закон сохранения энергии в тепловых процессах
Чтобы закон сохранения энергии для тепловых процессов был сформулирован, было сделано два важных шага. Сначала французский математик и физик Жан Батист Фурье установил один из основных законов теплопроводности. А потом Сади Карно определил, что тепловую энергию можно превратить в механическую.
Вот что сформулировал Фурье:
При переходе теплоты от более горячего тела к более холодному температуры тел постепенно выравниваются и становятся едиными для обоих тел — наступает состояние термодинамического равновесия.
Таким образом, первым важным открытием было открытие того факта, что все протекающие без участия внешних сил тепловые процессы необратимы.
Дальше Карно установил, что тепловую энергию, которой обладает нагретое тело, непосредственно невозможно превратить в механическую энергию для производства работы. Это можно сделать, только если часть тепловой энергии тела с большей температурой передать другому телу с меньшей температурой и, следовательно, нагреть его до более высокой температуры.
Закон сохранения энергии в тепловых процессах
При теплообмене двух или нескольких тел абсолютное количество теплоты, которое отдано более нагретым телом, равно количеству теплоты, которое получено менее нагретым телом.
Математически его можно описать так:
Уравнение теплового баланса
Qотд = Qпол
Qотд — отданное системой количество теплоты [Дж]
Qпол — полученное системой количество теплоты [Дж]
Данное равенство называется уравнением теплового баланса. В реальных опытах обычно получается, что отданное более нагретым телом количество теплоты больше количества теплоты, полученного менее нагретым телом:
Это объясняется тем, что некоторое количество теплоты при теплообмене передаётся окружающему воздуху, а ещё часть — сосуду, в котором происходит теплообмен.
Чтобы разобраться в задачках, читайте нашу статью про агрегатные состояния вещества.
Задачка раз
Сколько граммов спирта нужно сжечь в спиртовке, чтобы нагреть на ней воду массой 580 г на 80 °С, если учесть, что на нагревание пошло 20% затраченной энергии.
Удельная теплота сгорания спирта 2,9 · 107 Дж/кг, удельная теплоёмкость воды 4200 Дж/(кг · °С).
Решение:
При нагревании тело получает количество теплоты
Q = cmΔt ,
где c — удельная теплоемкость вещества
При сгорании тела выделяется энергия
Qсгор = q · mсгор,
где q — удельная теплота сгорания топлива
По условию задачи нам известно, что на нагревание воды пошло 20% энергии, полученной при горении спирта.
То есть:
Ответ: масса сгоревшего топлива равна 33,6 г.
Задачка два
Какое минимальное количество теплоты необходимо для превращения в воду 500 г льда, взятого при температуре −10 °С? Потерями энергии на нагревание окружающего воздуха пренебречь. Удельная теплоемкость льда равна 2100 Дж/кг · ℃, удельная теплота плавления льда равна 3,3 · 105 Дж/кг.
Решение:
Для нагревания льда до температуры плавления необходимо:
Qнагрев = cmΔt
Qнагрев = 2100 · 0,5 · (10 − 0) = 10 500 Дж
Для превращения льда в воду:
Qпл = λm
Qпл = 3,3 · 105 · 0,5 = 165 000 Дж
Таким образом, для превращения необходимо затратить:
Q = Qнагрев + Qпл = 10 500 + 165 000 = 175 500 Дж = 175,5 кДж
Ответ: чтобы превратить 0,5 кг льда в воду при заданных условиях необходимо 175,5 кДж тепла.
Энергия. Кинетическая энергия и её изменение
Физика10 класс
Материалы к уроку
-
19. Энергия. Кинетическая энергия и её изменение.doc
48 KBСкачать
-
19. Энергия. Кинетическая энергия и её изменение.ppt
11.23 MBСкачать
Конспект урока
Для совершения работы необходимо, чтобы на движущееся тело действовала та или иная сила. Тепловые двигатели обеспечивают действие силы до тех пор, пока не кончится топливо, электродвигатель — до тех пор, пока к нему подводится ток. Однако эти двигатели достаточно сложны.
Рассмотрим более простые системы движущихся тел, которые взаимодействуют между собой посредством сил тяготения и способны в той или иной мере деформироваться. Например, такие тела, как пружина или резиновый шнур, деформируются значительно. Каменные, деревянные, металлические тела деформируются так незначительно, что их деформациями обычно можно пренебречь. Будем считать, что никаких химических превращений тел не происходит, и что в системе нет заряженных тел и электрических токов. Можно заметить, что поднятые над землей грузы, а также системы, имеющие сжатые пружины, способны действовать на движущееся тело и совершать работу. Но способность таких тел совершать работу сохраняется лишь в течение определенного промежутка времени.
Растянутая пружина, сжимаясь, совершает работу, например, закрывает дверь. Эту работу пружина может совершать только в растянутом состоянии. Как только пружина сожмется до первоначального состояния, силы перестанут совершать работу.
На поднятый на какую-то высоту груз, действуют силы тяготения. Эти силы могут совершить работу – переместить груз вниз. Эта работа может быть совершена только в течение небольшого промежутка времени. Рано или поздно груз опустится на землю и силы перестанут совершать работу.
Совершение работы не проходит для системы тел бесследно. Рассмотрим, например, часы с пружинным заводом. При заводе часов состояние системы (часового механизма) меняется так, что она приобретает способность совершать работу в течение длительного времени. Пружина поддерживает движение всех колес, стрелок и маятника, испытывающих сопротивление движению, вызванное трением. По мере хода часов способность пружины совершать работу постепенно утрачивается. Состояние пружины меняется.
Подобным образом при совершении работы меняется состояние сжатого газа и скоростей движущихся тел.
Совершая механическую работу, тело или система тел переходят из одного состояния в другое, в котором их энергия минимальна. Растянутая пружина на двери распрямляется – дверь перестает двигаться. Чугунная баба копра опускается и останавливается. Пружина часов распрямляется – стрелки часов останавливаются. При совершении работы энергия постепенно расходуется. Для того чтобы система опять приобрела способность совершать работу, надо изменить ее состояние: растянуть пружину на двери, поднять бабу копра вверх, завертеть пружину часов. Для этого внешние силы должны совершить над системой положительную работу.
Энергия характеризует способность тела или системы тел совершать работу.
Энергия в механике – величина, определяемая состоянием системы — положением тел и их скоростями; изменение энергии при переходе системы из одного состояния в другое равно работе внешних сил.
В механике состояние системы определяется положением тел и их скоростями. Сначала выясним, как энергия тел зависит от их скоростей.
Подсчитаем работу постоянной силы, действующей на тело с определенной массой при его прямолинейном движении. Пусть направление силы совпадает с направлением скорости тела. В этом случае направления вектора перемещения и вектора
силы совпадают. Поэтому работа силы равна произведению модуля вектора силы на модуль перемещения тела.
Выберем координатную ось ОХ так, чтобы векторы силы начальной скорости, конечной скорости и перемещения были направлены в сторону положительного направления этой оси.
Тогда изменение вектора перемещения будет равно изменению координаты Х, и формулу для работы можно записать так: работа, совершаемая силой, равна произведению модуля вектора силы на изменение координаты тела.
Так как точка движется с постоянным ускорением, то изменение ее координаты при переходе из начального положения в конечное можно найти по известной нам из кинематики формуле: изменение координаты тела равно сумме произведения вектора начальной скорости на время и полупроизведению вектора ускорения на квадрат скорости или отношению разности квадратов конечной и начальной скоростей к удвоенному вектору ускорения.
Подставляя эту формулу в формулу работы и учитывая второй закон Ньютона, получим: работа равна произведению массы тела на его ускорение и на отношение разности квадратов конечной и начальной скоростей к удвоенному вектору ускорения. Проведя некоторые математические преобразования, получаем, что работа равна разности двух величин: полупроизведения массы тела на квадрат его конечной скорости и полупроизведения массы тела на квадрат его начальной скорости, то есть изменению полупроизведения массы тела и квадрата его скорости.
Эта формула, выведенная для случая прямолинейного движения тела, на которое действует постоянная сила, справедлива и в тех случаях, когда на тело действует переменная сила и оно движется по криволинейной траектории.
Величина, равная полупроизведению массы тела на квадрат его скорости представляет собой энергию, которую имеет тело, движущееся с конкретной скоростью. Эту энергию называют кинетической, от греческого слова «кинема» — движение.
Кинетическая энергия тела равна половине произведения массы тела на квадрат его скорости.
Энергия измеряется в тех же единицах, что и работа, в джоулях.
Полученную нами формулу работы можно записать так: работа равна изменению кинетической энергии. Это равенство выражает теорему об изменении кинетической энергии: изменение кинетической энергии тела (материальной точки) за некоторый промежуток времени равно работе, совершенной за то же время силой, действующей на тело.
Если на тело действует несколько сил, то изменение его кинетической энергии равно сумме работ всех сил, действующих на тело.
Кинетическая энергия тел зависит только от их масс и скоростей. Полная механическая энергия системы зависит от скоростей тел и расстояний между ними. Для того чтобы вычислить ту часть энергии, которая зависит от расстояний между телами, нужно предварительно рассмотреть вопрос о работе силы тяжести и силы упругости.
Движущееся тело обладает кинетической энергией. Эта энергия равна работе, которую надо совершить, чтобы увеличить скорость тела от нуля до определенного значения.
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ

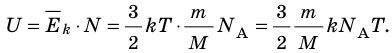 Итак, для одноатомного идеального газа:
Итак, для одноатомного идеального газа: 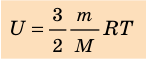 . Используя уравнение состояния
. Используя уравнение состояния 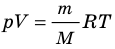 , выражение для внутренней энергии идеального одноатомного газа можно представить так:
, выражение для внутренней энергии идеального одноатомного газа можно представить так: