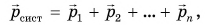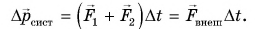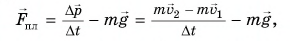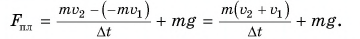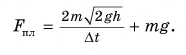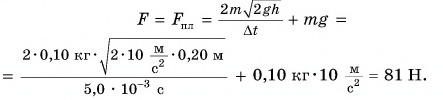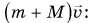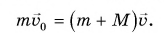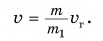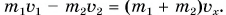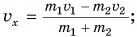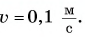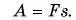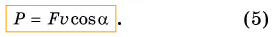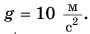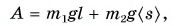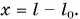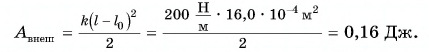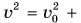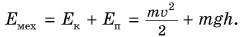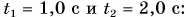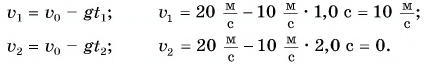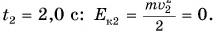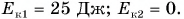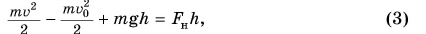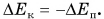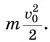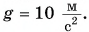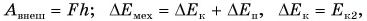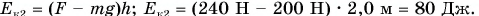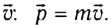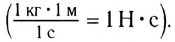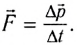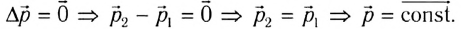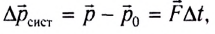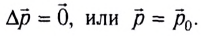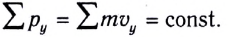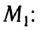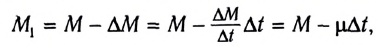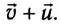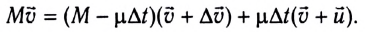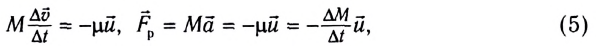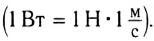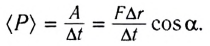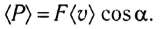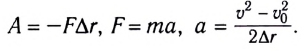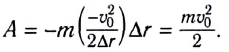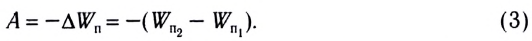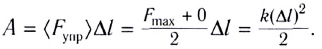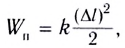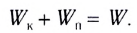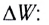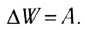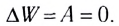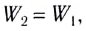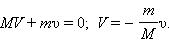I. Механика
Тестирование онлайн
Импульс тела
Пуля 22-го калибра имеет массу всего 2 г. Если кому-нибудь бросить такую пулю, то он легко сможет поймать ее даже без перчаток. Если же попытаться поймать такую пулю, вылетевшую из дула со скоростью 300 м/с, то даже перчатки тут не помогут.
Если на тебя катится игрушечная тележка, ты сможешь остановить ее носком ноги. Если на тебя катится грузовик, следует уносить ноги с его пути.
Импульс это векторная величина, которая определяется по формуле
Импульс служит мерой того, насколько велика должна быть сила, действующая в течение определенного времени, чтобы остановить или разогнать его с места до данной скорости.
Направление вектора импульса всегда совпадает с направлением вектора скорости.
Если тело покоится, импульс равен нулю. Ненулевым импульсом обладает любое, движущееся тело. Например, когда мяч покоится, его импульс равен нулю. После удара он приобретает импульс. Импульс тела изменяется, так как изменяется скорость.
Импульс силы
Это векторная величина, которая определяется по формуле
Изменение импульса тела равно импульсу равнодействующей всех сил, действующих на тело. Это иная формулировка второго закона Ньютона
Рассмотрим задачу, которая демонстрирует связь импульса силы и изменения импульса тела.
Пример. Масса мяча равна 400 г, скорость, которую приобрел мяч после удара — 30 м/с. Сила, с которой нога действовала на мяч — 1500 Н, а время удара 8 мс. Найти импульс силы и изменение импульса тела для мяча.
Изменение импульса тела
Как определить изменение импульса тела? Необходимо найти численное значение импульса в один момент времени, затем импульс через промежуток времени. От второй найденной величины отнять первую. Внимание! Вычитать надо вектора, а не числа. То есть из второго вектора импульса отнять первый вектор. Смотрите вычитание векторов.
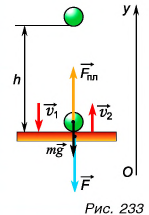
Пример. Оценить среднюю силу со стороны пола, действующую на мяч во время удара.
1) Во время удара на мяч действуют две силы: сила реакции опоры, сила тяжести.
Сила реакции изменяется в течение времени удара, поэтому возможно найти среднюю силу реакции пола.
2) Изменение импульса 
3) Из второго закона Ньютона
Главное запомнить
1) Формулы импульса тела, импульса силы;
2) Направление вектора импульса;
3) Находить изменение импульса тела
Вывод второго закона Ньютона в общем виде
График F(t). Переменная сила
Уже в течение длительного
времени мы с вами рассматриваем три закона Ньютона, которые позволяют решать большой
спектр задач по движению и взаимодействию тел. Причём многие из задач связаны с
нахождением ускорения движущегося тела по известным действующим силам.
Однако при взаимодействии тел
могут непрерывно изменяться не только их координаты и скорости, но и силы,
действующие между телами. В этом случае бывает очень сложно их определить. Для
описания подобных ситуаций в механике были введены специальные величины, одной
из которых является импульс.
Импульсом тела называется
произведение массы тела на скорость его движения.
Импульс тела (его также
называют количеством движения) — это векторная величина. Так как масса тела
величина скалярная и всегда больше нуля, то направление вектора импульса
совпадает с направлением вектора скорости тела, но он в т раз его больше.
Единица импульса в СИ — это килограмм на метр в секунду:
Понятие импульса было введено в
науку французским учёным Рене Декартом. Так как понятие массы ещё не было, то
Декарт определял импульс как произведение величины тела на скорость его
движения.
Позже, в математических
началах натуральной философии Ньютон уточнил понятие импульса: количество
движения есть мера токового, устанавливаемая пропорционально скорости и массе.
Из первого закона Ньютона
следует, что скорость свободного тела, а значит, и его импульс постоянны. Значит,
импульс тела можно изменить только приложив к нему силу.
Рассмотрим простой пример.
Тележку известной массы и имеющей некоторую начальную скорость разгоняют под
действием постоянной силы в течение небольшого промежутка времени. Определим,
на сколько измениться импульс тележки.
Так как в данном случае силами
сопротивления движению можно пренебречь, а сила тяжести тележки и сила
упругости опоры компенсируют друг друга, то
В общем случае изменение
импульса тела равно произведению результирующей всех сил, приложенных к телу,
на время её действия. В этом заключается закон изменения импульса тела.
Отметим, что произведение
силы на время её действия, называют импульсом силы. А единицей импульса
силы в СИ является ньютон на секунду:
Из закона изменения импульса
тела следует, что изменение количества движения пропорционально приложенной движущей
силе и происходит по прямой, по которой эта сила действует. Это соотношение
выражает второй закон Ньютона в той формулировке, которая была дана самим
Ньютоном.
Закон изменения импульса
объясняет целый ряд явлений повседневной жизни. Проделаем простой опыт. Возьмём
две нити: обычную и резиновую одинаковой прочности и длины. Привяжем их к
одинаковым грузам и дадим им возможность падать с одинаковой высоты. Простая
нить порвётся, а резиновая нить — нет.
Почему это происходит? Дело в
том, что время торможения для груза на обычной нити было во много раз меньше,
чем для груза на резиновой, легко деформируемой нити. А из второго закона
Ньютона следует, что сила тем больше, чем меньше время её действия (при равных
изменениях импульса).
Поэтому, например, чтобы
избежать тяжёлых последствий при столкновениях, следует увеличить время, за
которое «гасится» импульс. Для этого вагоны снабжают буферными пружинными
амортизаторами, автомобили — бамперами, ремнями безопасности и автоматически
срабатывающими воздушными подушками.
И наоборот, для получения
больших сил используют удар, при котором импульс изменяется очень быстро.
Примерами служат забивание свай падающим «молотом», разрушающее действие пуль,
снарядов и так далее.
Мы рассмотрели изменение импульса
одного тела. А как изменяется суммарный импульс нескольких тел?
Итак, пусть у нас есть два
одинаковых шарика, подвешенных на нитяных петлях. Отклоним один из шариков на
некоторый угол и отпустим его. Вернувшись в своё первоначальное положение, он ударит
по второму шарику и остановиться. При этом второй шарик придёт в движение и
отклониться от своего первоначального положения на тот же угол, на который мы
отклонили первый шарик.
В дальнейшем такое движение
будет продолжаться. Очевидно, что в данном случае в результате взаимодействия
шаров импульс каждого из них постоянно меняется. Причём, на сколько уменьшается
импульс одного шара, на столько же увеличивается импульс другого.
В механике группу из
нескольких тел называют механической системой. Если тела, входящие в
механическую систему, взаимодействуют только между собой, то такая система
называется замкнутой.
Каждое из тел механической
системы имеет свой импульс. Векторная сумма импульсов всех тел, входящих в
систему, называется импульсом механической системы.
Как мы убедились на опыте,
импульс каждого из тел, входящих в замкнутую систему, может меняться в
результате взаимодействия тел друг с другом, но векторная сумма импульсов
тел, составляющих замкнутую систему, не меняется с течением времени при любых
взаимодействиях тел системы. В этом и заключается один из фундаментальных
законов природы — закон сохранения импульса.
Конечно же реальные системы
никогда не бывают полностью замкнутыми. Внешние тела всегда в той или иной мере
влияют на рассматриваемую систему. Мы знаем, что на все окружающие тела
действует Земля, на систему Земля — Луна действует Солнце и другие планеты, а на
Солнечную систему — звезды Галактики. Однако закон сохранения импульса с
успехом применяют и для незамкнутых систем.
— В каких случаях это можно
делать?
Во-первых, если внешние
силы действуют, но их результирующая равна нулю. Для примера рассмотрим
движение двух упругих шаров по гладкой горизонтальной поверхности. Так как шары
движутся на встречу друг другу, то через некоторое время произойдёт их
столкновение, длящееся очень малый промежуток времени. В результате скорости
шаров изменятся. Так как в вертикальном направлении на каждый из шаров
действуют сила тяжести со стороны Земли и сила реакции опоры, то в этом
направлении систему нельзя считать замкнутой. В горизонтальном же направлении
силой трения можно пренебречь, поэтому систему из двух взаимодействующих шаров
можно считать замкнутой в этом направлении.
Полученные нами уравнения
выражают математическую запись закона сохранения импульса.
Закон сохранения импульса
применим и тогда, когда внутренние силы намного больше внешних. Это относится к соударениям тел, выстрелам, взрывам и
тому подобное.
Кроме того, для незамкнутых
систем можно применять закон сохранения проекции импульса. Покажем это. Для
чего рассмотрим соударение шарика с гладкой горизонтальной поверхностью.
Значит, проекция импульса
системы на ось, перпендикулярную внешней силе, не изменяется.
А теперь давайте проверим
выполнимость закона сохранения импульса экспериментально. Для этого проведём
опыт с системой, состоящей из тележки с закреплённым на ней ящиком с песком, и
шара. Пустим по наклонному жёлобу шар так, чтобы он попал в ящик с песком.
Тележка начала двигаться в ту сторону, куда двигался шар.
В следующем опыте на
покоящуюся тележку по двум одинаковым наклонным желобам с одинаковых высот
спустим два одинаковых шара. Шары одновременно падают в песок. Но тележка
остаётся в состоянии покоя. Попробуйте самостоятельно объяснить результаты этих
опытов.
Закрепления материала.
Если на тело массой m за определенный промежуток времени Δt действует сила F→, тогда следует изменение скорости тела ∆v→=v2→-v1→. Получаем, что за время Δt тело продолжает движение с ускорением:
a→=∆v→∆t=v2→-v1→∆t.
Основываясь на основном законе динамики, то есть втором законе Ньютона, имеем:
F→=ma→=mv2→-v1→∆t или F→∆t=mv2→-mv1→=m∆v→=∆mv→.
Изменение импульса
Импульс тела, или количество движения – это физическая величина, равная произведению массы тела на скорость его движения.
Импульс тела считается векторной величиной, которая измеряется в килограмм-метр в секунду (кг м/с).
Импульс силы – это физическая величина, равняющаяся произведению силы на время ее действия.
Импульс относят к векторным величинам. Существует еще одна формулировка определения.
Изменение импульса тела равняется импульсу силы.
При обозначении импульса p→ второй закон Ньютона записывается как:
F→∆t=∆p→.
Данный вид позволяет формулировать второй закон Ньютона. Сила F→ является равнодействующей всех сил, действующих на тело. Равенство записывается как проекции на координатные оси вида:
FxΔt=Δpx; FyΔt=Δpy; FzΔt=Δpz.
Рисунок 1.16.1. Модель импульса тела.
Изменение проекции импульса тела на любую из трех взаимно перпендикулярных осей равно проекции импульса силы на эту же ось.
Одномерное движение – это движение тела по одной из координатный осей.
На примере рассмотрим свободное падение тела с начальной скоростью v0 под действием силы тяжести за промежуток времени t. При направлении оси OY вертикально вниз импульс силы тяжести Fт=mg, действующий за время t, равняется mgt. Такой импульс равняется изменению импульса тела:
Fтt=mgt=Δp=m(v–v0), откуда v=v0 + gt.
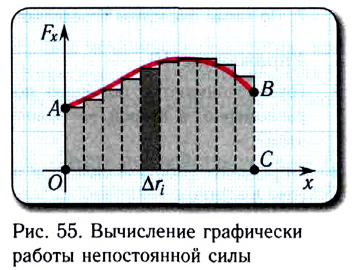
Запись совпадает с кинематической формулой определения скорости равноускоренного движения. По модулю сила не изменяется из всего интервала t. Когда она изменяема по величине, тогда формула импульса требует подстановки среднего значения силы Fср из временного промежутка t. Рисунок 1.16.2 показывает, каким образом определяется импульс силы, которая зависит от времени.
Рисунок 1.16.2. Вычисление импульса силы по графику зависимости F(t)
Необходимо выбрать на временной оси интервал Δt, видно, что сила F(t) практически неизменна. Импульс силы F(t)Δt за промежуток времени Δt будет равняться площади заштрихованной фигуры. При разделении временной оси на интервалы на Δti на промежутке от от 0 до t, сложить импульсы всех действующих сил из этих промежутков Δti, тогда суммарный импульс силы будет равняться площади образования при помощи ступенчатой и временной осей.
Применив предел (Δti→0), можно найти площадь, которая будет ограничиваться графиком F(t) и осью t. Использование определения импульса силы по графику применимо с любыми законами, где имеются изменяющиеся силы и время. Данное решение ведет к интегрированию функции F(t) из интервала [0; t].
Рисунок 1.16.2 показывает импульс силы, находящийся на интервале от t1=0 с до t2=10.
Из формулы получим, что Fср(t2-t1)=12Fmax(t2-t1)=100 Н·с=100 кг·м/с.
То есть, из примера видно Fср=12Fmax=10 Н.
Определение средней силы
Имеются случаи, когда определение средней силы Fср возможно при известных времени и данных о сообщенном импульсе. При сильной ударе по мячу с массой 0,415 кг можно сообщить скорость, равную v=30 м/с. Приблизительным временем удара является значение 8·10–3 с.
Тогда формула импульса приобретает вид:
p=mv=12,5 кг·м/с.
Чтобы определить среднюю силу Fср во время удара, необходимо Fср=p∆t=1,56·103 Н.
Получили очень большое значение, которое равняется телу массой 160 кг.
Когда движение происходит по криволинейной траектории, то начальное значение p1→ и конечное
p2→ могут быть различны по модулю и по направлению. Для определения импульса ∆p→ применяют диаграмму импульсов, где имеются векторы p1→ и p2→, а ∆p→=p2→-p1→ построен по правилу параллелограмма.
Для примера приводится рисунок 1.16.2, где нарисована схема импульсов мяча, отскакивающего от стены. При подаче мяч с массой m со скоростью v1→ налетает на поверхность под углом α к нормали и отскакивает со скоростью v2→ с углом β. При ударе в стену мяч подвергался действию силы F→, направленной также, как и вектор ∆p→.
Рисунок 1.16.3. Отскакивание мяча от шероховатой стенки и диаграмма импульсов.
Если происходит нормальное падение мяча с массой m на упругую поверхность со скоростью v1→=v→, тогда при отскоке она изменится на v2→=-v→. Значит, за определенный промежуток времени импульс изменится и будет равен ∆p→=-2mv→. Используя проекции на ОХ, результат запишется как Δpx=–2mvx. Из рисунка 1.16.3 видно, что ось ОХ направлена от стенки, тогда следует vx<0 и Δpx>0. Из формулы получим, что модуль Δp связан с модулем скорости, который принимает вид Δp=2mv.
Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:
p = mv
Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).
Направление импульса всегда совпадает с направлением скорости (p↑↓v), так как масса — всегда положительная величина (m > 0).
Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.
Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:
10 г = 0,01 кг
Импульс равен:
p = mv = 0,01∙300 = 3 (кг∙м/с)
Относительный импульс
Определение
Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:
p1отн2 = m1v1отн2 = m1(v1 – v2)
p1отн2 — импульс первого тела относительно второго, m1 — масса первого тела, v1отн2 — скорость первого тела относительно второго, v1 и v2 — скорости первого и второго тела соответственно в одной и той же системе отсчета.
Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.
Сначала переведем единицы измерения в СИ:
15 т = 15000 кг
p1отн2 = m1(v1 – v2) = 15000(20 – 15) = 75000 (кг∙м/с) = 75∙103 (кг∙м/с)
Изменение импульса тела
ОпределениеИзменение импульса тела — векторная разность между конечным и начальным импульсом тела:
∆p = p – p0 = p + (– p0)
∆p — изменение импульса тела, p — конечный импульс тела, p0 — начальный импульс тела
Частные случаи определения изменения импульса тела
Абсолютно неупругий удар |
|
|
|
Конечная скорость после удара:
v = 0. Конечный импульс тела: p = 0. Модуль изменения импульса тела равен модулю его начального импульса: ∆p = p0. |
Абсолютно упругий удар |
|
|
|
Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p. |
Пуля пробила стенку |
|
|
|
Модуль изменения импульса тела равен разности модулей начального и конечного импульсов: ∆p = p0 – p = m(v0 – v) |
Радиус-вектор тела повернул на 180 градусов |
|
|
|
Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p = 2mv0 |
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали |
|
|
|
Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Угол падения равен углу отражения: α = α’ Модуль изменения импульса в этом случае определяется формулой: |
Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.
В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.
Вычисляем:
Второй закон Ньютона в импульсном виде
Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:
Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:
Подставим это выражение во второй закон Ньютона и получим:
Или:
F∆t — импульс силы, ∆p — изменение импульса тела
Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?
Из формулы импульса силы выразим модуль силы:
Реактивное движение
Определение
Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.
Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.
Второй закон Ньютона в импульсном виде:
Реактивная сила:
Второй закон Ньютона для ракеты:
Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.
Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:
V = a∆t
Выразим ускорение из второго закона Ньютона для ракеты:
Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет вид:
Отсюда ускорение равно:
Выразим формулу для скорости и сделаем вычисления:
Суммарный импульс системы тел
Определение
Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:
Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.
Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:
Закон сохранения импульса
Закон сохранения импульсаПолный импульс замкнутой системы сохраняется:
Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.
Закон сохранения импульса в проекции на горизонтальную ось
Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:
- положителен, если его направление совпадает с направлением оси ОХ;
- отрицателен, если он направлен противоположно направлению оси ОХ.
Важно!
При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.
Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)
| Неупругое столкновение с неподвижным телом | m1v1 = (m1 + m2)v |
| Неупругое столкновение движущихся тел | ± m1v1 ± m2v2 = ±(m1 + m2)v |
| В начальный момент система тел неподвижна | 0 = m1v’1 – m2v’2 |
| До взаимодействия тела двигались с одинаковой скоростью | (m1 + m2)v = ± m1v’1 ± m2v’2 |
Сохранение проекции импульса
В незамкнутых системах закон сохранения импульса выполняется частично. Например, если из пушки под некоторым углом α к горизонту вылетает снаряд, то влияние силы реакции опоры не позволит орудию «уйти под землю». В момент отдачи оно будет откатываться от поверхности земли.
Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.
Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:
m2v2 = (m1 + m2)v
Отсюда скорость равна:
Задание EF17556
Импульс частицы до столкновения равен −p1, а после столкновения равен −p2, причём p1 = p, p2 = 2p, −p1⊥−p2. Изменение импульса частицы при столкновении Δ−p равняется по модулю:
а) p
б) p√3
в) 3p
г) p√5
Алгоритм решения
1.Записать исходные данные.
2.Построить чертеж, обозначить векторы начального и конечного импульсов, а также вектор изменения импульса. Для отображения вектора изменения импульса использовать правило сложения векторов методом параллелограмма.
3.Записать геометрическую формулу для вычисления длины вектора изменения импульса.
4.Подставить известные значения и вычислить.
Решение
Запишем исходные данные:
• Модуль импульса частицы до столкновения равен: p1 = p.
• Модуль импульса частицы после столкновения равен: p2 = 2p.
• Угол между вектором начального и вектором конечного импульса: α = 90о.
Построим чертеж:
Так как угол α = 90о, вектор изменения импульса представляет собой гипотенузу треугольника, катами которого являются вектора начального и конечного импульсов. Поэтому изменение импульса можно вычислить по теореме Пифагора:
Δp=√p21+p22
Подставим известные данные:
Δp=√p2+(2p)2=√5p2=p√5
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17695

а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно
б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено
в) в интервалах 0–1 и 1–2 двигалось равномерно
г) в интервалах 0–1 и 1–2 двигалось равноускорено
Алгоритм решения
1.Записать формулу, связывающую импульс тема с его кинематическими характеристиками движения.
2.Сделать вывод о том, как зависит характер движения от импульса.
3.На основании вывода и анализа графика установить характер движения тела на интервалах.
Решение
Импульс тела есть произведение массы тела на его скорость:
p = mv
Следовательно, импульс и скорость тела — прямо пропорциональные величины. Если импульс с течением времени не меняется, то скорость тоже. Значит, движение равномерное. Если импульс растет линейно, то и скорость увеличивается линейно. В таком случае движение будет равноускоренным.
На участке 0–1 импульс тела не менялся. Следовательно, на этом участке тело двигалось равномерно. На участке 1–2 импульс тела увеличивался по линейной функции, следовательно, на этом участке тело двигалось равноускорено.
Верный ответ: б.
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF22730

Алгоритм решения
1.Записать исходные данные.
2.Записать закон сохранения импульса применительно к задаче.
3.Записать формулу кинетической энергии тела.
4.Выполнить общее решение.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса камня: m1 = 3 кг.
• Масса тележки с песком: m2 = 15 кг.
• Кинетическая энергия тележки с камнем: Ek = 2,25 Дж.
Так как это абсолютно неупругий удар, закон сохранения импульса принимает вид:
m1v1+m2v2=(m1+m2)v
Учтем, что скорость тележки изначально была равна нулю, а к ее движению после столкновения привела только горизонтальная составляющая начальной скорости камня:
m1v1cosα=(m1+m2)v
Выразить конечную скорость системы тел после столкновения мы можем через ее кинетическую энергию:
Ek=(m1+m2)v22
Отсюда скорость равна:
v=√2Ekm1+m2
Выразим скорость камня до столкновения через закон сохранения импульса и подставим в формулу найденную скорость:
v1=(m1+m2)vm1cosα=(m1+m2)m1cosα·√2Ekm1+m2
Подставим известные данные и произведем вычисления:
v1=(3+15)3cos60o·√2·2,253+15=12·√0,25=12·0,5=6 (мс)
Ответ: 6
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF22520

. Импульс второго осколка изображается вектором:
а) −−→AB
б) −−→BC
в) −−→CO
г) −−→OD
Алгоритм решения
1.Сформулировать закон сохранения импульса и записать его в векторной форме.
2.Применить закон сохранения импульса к задаче.
3.Выразить из закона импульс второго осколка и найти на рисунке соответствующий ему вектор.
Решение
Согласно закону сохранения импульса, импульс замкнутой системы тел сохраняется. Записать его можно так:
−p1+−p2=−p′
1+−p′2
Можем условно считать осколки замкнутой системой, так как они не взаимодействуют с другими телами. Применяя к ним закон сохранения импульса, получим:
−p0=−p1+−p2
Отсюда импульс второго осколка равен векторной разности импульса снаряда и импульса первого осколка:
−p2=−p0−−p1
Известно, что разностью двух векторов является вектор, начало которого соответствует вычитаемому вектору, а конец — вектору уменьшаемому. В нашем случае вычитаемый вектор — вектор импульса первого осколка. Следовательно, начало вектора импульса второго осколка лежит в точке А. Уменьшаемый вектор — вектор импульса снаряда. Следовательно, конец вектора лежит в точке В. Следовательно, искомый вектор — −−→AB.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18122
Летящая горизонтально со скоростью 20 м/с пластилиновая пуля массой 9 г попадает в груз неподвижно висящий на нити длиной 40 см, в результате чего груз с прилипшей к нему пулей начинает совершать колебания. Максимальный угол отклонения нити от вертикали при этом равен α = 60°. Какова масса груза?
Ответ:
а) 27 г
б) 64 г
в) 81 г
г) 100 г
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Сделать чертеж, отобразив начальное, промежуточное и конечное положение тел.
3.Записать закон сохранения импульса для момента столкновения и закон сохранения механической энергии для момента максимального отклонения нити от положения равновесия.
4.Выполнить решение задачи в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса пластилиновой пули: m = 9 г.
• Скорость пластилиновой пули: v = 20 м/с.
• Максимальный угол отклонения нити: α = 60°.
Переведем единицы измерения величин в СИ:
Сделаем чертеж:
Нулевой уровень — точка А.
После неупругого столкновения пули с грузом они начинают двигаться вместе. Поэтому закон сохранения импульса для точки А выглядит так:
mv=(m+M)V
После столкновения система тел начинается двигаться по окружности. Точка В соответствует верхней точке траектории. В этот момент скорость системы на мгновение принимает нулевое значение, а потенциальная энергия — максимальное.
Закон сохранения энергии для точки В:
(m+M)V22=(m+M)gh
V22=gh
Высоту h можно определить как произведение длины нити на косинус угла максимального отклонения. Поэтому:
V=√2glcosα
Подставим это выражение в закон сохранения импульса для точки А и получим:
Выразим массу груза:
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | Просмотров: 18.1k
Содержание:
Три закона Ньютона являются основой механики. Выдающийся американский физик XX ст. P Фейнман в своих знаменитых «Фейнмановских лекциях» отметил, что вся классическая механика содержится в этих законах. C их помощью в принципе можно решить любую задачу о движении тел с малыми скоростями.
Значение законов Ньютона заключается не только в этом. Они позволили создать стройную физическую теорию механического движения тел, ввести такие фундаментальные физические величины, как энергия и импульс, установить для них законы сохранения, являющиеся фундаментальными законами природы. C помощью этих законов в динамике решаются задачи, когда силы взаимодействия тел неизвестны. Например, при столкновении тел трудно определить значения сил взаимодействия между ними.
Законы сохранения в механике
Все изменения, наблюдаемые нами в природе, -результат взаимодействия между телами. Взаимодействия бывают электромагнитные, гравитационные и ядерные. Их интенсивность зависит не только от их природы, но и от расстояний между телами, их характеристик.
При определенных условиях один вид взаимодействия может быть интенсивнее другого. Так, на больших расстояниях существенным является гравитационное взаимодействие, в то время как ядерное будет существенным только на расстояниях, соизмеримых с размерами ядра атома.
Одновременно сделать расчеты всех взаимодействий тяжело, да и не всегда нужно. Поэтому ученые, как правило, рассматривают физические явления, пренебрегая некоторыми второстепенными взаимодействиями. Например, при расчетах силы трения, действующей на колеса автомобиля, существенной является сила притяжения Земли, а действием Луны можно пренебречь.
Ученые, рассматривая физические явления, как правило, пренебрегают второстепенными взаимодействиями.
При расчетах движения межпланетного корабля в пределах Солнечной системы нельзя пренебречь действием на корабль Солнца и планет, а вот действие далеких звезд можно не принимать во внимание.
Таким образом, в общей картине природы рассматривается лишь некоторая совокупность физических тел, условно изолированных от окружающей среды и объединенных общими признаками.
Группа объединенных по общим признакам тел, на которые не действуют другие тела или их действие несущественно в данных условиях, называется замкнутой (изолированной) системой.
Замкнутость системы — понятие относительное и определяется задачами, которые ставятся перед исследованиями, и уровнем развития их экспериментального или теоретического методов решения. Если система по определенным соображениям объявляется замкнутой, то она не становится абсолютно изолированной, «вне природы», в ней действуют те же физические законы. Это подтверждается многочисленными исследованиями, свидетельствующими об однородности пространства. Ни одной точке пространства нельзя дать преимущество по сравнению с другими точками, а протекание физических явлений не изменяется в случае перехода из одной точки пространства в другую. Поэтому не случайно закон гравитационного взаимодействия называется всемирным.
Наличие однородности в полной мере присуще и времени. Течение времени в разных точках пространства происходит одинаково. Поэтому некоторые физические величины в замкнутых системах остаются неизменными, например масса, энергия, импульс, т. е. подчиняются законам сохранения. В механике основными такими законами являются закон сохранения энергии и закон сохранения импульса.
Импульс тела и импульс системы тел
Еще в XVII в. в механике появилось понятие «количество движения». В настоящее время количество движения тела называют импульсом тела (от латинского impulses — толчок). Чему он равен? Как его можно изменить?
В механике Ньютона импульсом тела называется векторная величина, равная произведению массы тела на скорость его движения:
Импульс тела направлен так же, как скорость движения тела. Единица импульса в СИ — I килограмм-метр в секунду
Из определения следует, что импульс зависит и от скорости, и от массы. Например, импульс груженого самосвала БЕЛАЗ гораздо больше импульса движущегося с такой же скоростью автомобиля (рис. 225).
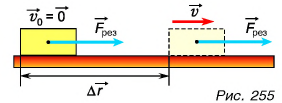
Согласно первому закону Ньютона скорость движения тела, на которое не действуют силы или действие сил скомпенсировано, постоянна. Значит, в этом случае постоянен и его импульс. Изменить импульс тела можно, только приложив к нему силу.
Рассмотрим пример. Тележку массой т, имеющую начальную скорость 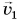
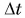
Найдем результирующую силу, действующую на тележку. Силами сопротивления можно пренебречь, сила реакции N и сила тяжести mg (рис. 226) компенсируют друг друга. Тогда по второму закону Ньютона
Подставляя в эту формулу ускорение 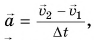
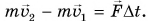
Величину 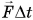
Импульс силы — это векторная величина, равная произведению силы на время ее действия.
Формула (2) выражает закон изменения импульса тела.
Изменение импульса тела равно импульсу результирующей всех сил, приложенных к нему.
Из данного закона следует:
- изменение импульса тела
направлено так же, как результирующая сила F;
- изменение импульса тела тем больше, чем больше приложенная к нему сила и чем продолжительнее время ее действия.
Формулу (2) можно записать в виде
Для любознательных:
Равенство 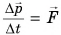
Закон изменения импульса объясняет целый ряд явлений повседневной жизни.
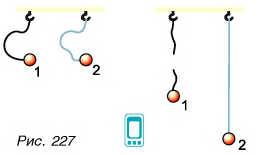
Проделаем простой опыт. Возьмем две нити: обычную 1 и резиновую 2 (рис. 227) одинаковой прочности и длины. Привяжем их к одинаковым грузам и дадим грузам возможность падать с одинаковой высоты. Нить 1 порвется, а нить 2 — нет (рис. 227). Почему это происходит?
Дело в том, что промежуток времени торможения At для груза на обычной нити 1 был во много раз меньше, чем для груза на резиновой, легко деформируемой нити 2. Из формулы (3) следует, что сила F тем больше, чем меньше 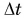
Это необходимо учитывать в технике. Нельзя делать резких рывков при подъеме грузов и при буксировке транспортных средств. Может произойти обрыв троса.
Чтобы избежать тяжелых последствий при столкновениях, следует уменьшить силу или увеличить время, за которое импульс уменьшится до нуля. Для этой цели вагоны снабжают буферными пружинными амортизаторами (рис. 228), автомобили — бамперами, ремнями безопасности, автоматически срабатывающими воздушными подушками (рис. 229).

И наоборот, для получения больших сил используют удар, при котором импульс изменяется за очень малый промежуток времени At (см. формулу (3)). Примерами служат забивание свай падающим молотом (рис. 230), разрушающее действие пуль, снарядов и т. д.
Мы рассмотрели изменение импульса одного тела. А как изменяется суммарный импульс нескольких тел?
В механике группу из нескольких тел называют механической системой. Тела, не входящие в систему, называются внешними телами.
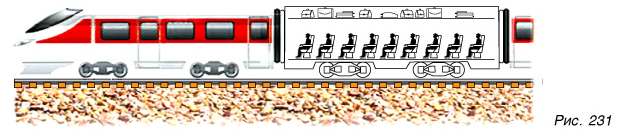
Например, механической системой является пассажирский вагон (рис. 231). В механическую систему «вагон» входят: корпус вагона, люди, находящиеся в вагоне, багаж и т. д. Внешними телами будут: Земля, локомотив, рельсы, остальные вагоны поезда и т. д.
Силы взаимодействия тел системы друг с другом называют внутренними. Например, в системе «вагон» внутренней будет сила, с которой багаж давит на полку, и сила, с которой полка действует на багаж. Силы, действующие на тела системы со стороны внешних тел, называют внешними силами. Например, сила тяжести, с которой Земля действует на багаж, — это внешняя сила.
Каждое из тел механической системы имеет свой импульс. Векторная сумма импульсов всех тел, входящих в систему, называется импульсом механической системы:
где п — количество тел системы.
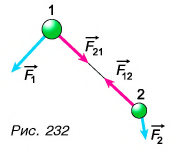
Рассмотрим систему из двух тел (1 и 2) (рис. 232). Силы их взаимодействия 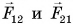
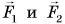
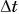
По третьему закону Ньютона силы взаимодействия тел
С учетом этого
А если в механическую систему входит больше двух тел? Сумма всех внутренних сил будет по-прежнему равна нулю, а изменение импульса механической системы
где 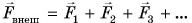
Формула (4) выражает закон изменения импульса механической системы.
Изменение импульса механической системы равно импульсу результирующей внешних сил.
Таким образом, только внешние силы могут вызвать изменение импульса механической системы. Внутренние силы не изменяют импульс механической системы в целом, но могут изменить импульс отдельных тел системы.
Ответьте самостоятельно: какая сила увеличивает импульс вагона на участке разгона? Какие силы уменьшают импульс вагона при его торможении? Могут ли пассажиры, находящиеся в вагоне, вызвать изменение импульса механической системы «вагон»?
Главные выводы:
- Импульс тела — это векторная величина, равная произведению массы тела на скорость его движения.
- Направление импульса тела совпадает с направлением его скорости.
- Изменение импульса тела равно импульсу результирующей всех сил, приложенных к нему.
- Изменить импульс механической системы могут только внешние силы. Это изменение равно импульсу результирующей внешних сил.
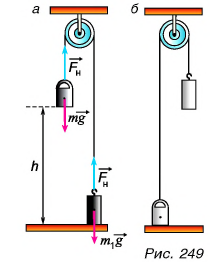
Пример №1
Шарик массой 
Решение

Так как на шарик во время удара действуют сила тяжести и сила, приложенная к нему со стороны плиты, то изменение импульса шарика за время удара 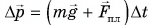
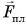
где 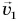
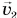
В проекции на ось Оу.
Так как шарик свободно падал без начальной скорости с высоты h, то 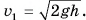
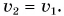
По третьему закону Ньютона средняя сила, с которой шарик во время удара действовал на плиту, 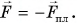
Сила, с которой шарик во время удара действовал на плиту, направлена по вертикали вниз. Модуль средней силы удара в 81 раз больше, чем вес покоящегося шарика.
Закон сохранения импульса и реактивное движение
Знаменитый французский философ и математик Рене Декарт (1596— 1650) утверждал: «Во Вселенной есть известное количество движения, которое никогда не изменяется. И если одно тело приводит в движение другое, то оно теряет столько своего движения, сколько его сообщает». Как вывести это утверждение из закона изменения импульса?
В предыдущем параграфе мы доказали, что импульс системы тел может измениться только под действием внешних сил:
А если результирующая внешних сил 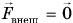
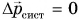
Векторное равенство (2) выражает закон сохранения импульса. Импульс механической системы сохраняется, если результирующая внешних сил, действующих на нее, равна нулю.
В каких случаях можно применять закон сохранения импульса? Прежде всего — когда на систему вообще не действуют внешние силы. Такие системы называют замкнутыми. Импульс замкнутой системы не изменяется (сохраняется), как и утверждал Декарт.
Реальные механические системы не бывают замкнутыми. На все окружающие нас тела действует Земля, на Землю действует Солнце и т. д. Однако закон сохранения импульса можно применять и для незамкнутых систем, если:
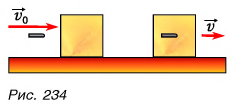
Например, закон сохранения импульса применяют при решении задач о столкновениях тел, выстрелах и т. д., когда в течение крайне малых промежутков времени внутри системы возникают огромные силы. Рассмотрим пример. Деревянный кубик массой М лежит на горизонтальном столе. В кубик попадает пуля массой 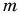
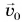
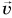
Замкнута ли система «кубик + пуля»? Нет. Но сила тяжести системы скомпенсирована силой реакции опоры, а сила трения кубика о стол мала. Значит, величиной 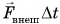
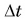
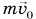
Значит, скорость кубика вместе с пулей после удара
Соударение, в результате которого тела объединяются и ведут себя как единое целое, называют абсолютно неупругим ударом.
Рассмотренный пример — частный случай такого удара. Другими примерами являются соединение вагонов при сценке, слипание пластилиновых шариков при соударении и т. д.
Рассмотрим теперь пример, в котором происходит не объединение, а разделение частей системы.
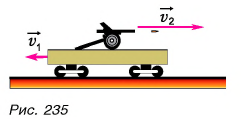
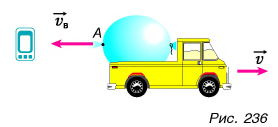
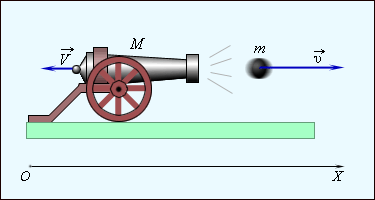
На горизонтальном рельсовом пути стоит платформа (рис. 235) с закрепленной на ней пушкой. Установка может свободно катиться по рельсам. Ствол орудия горизонтален. Пушка производит выстрел. Платформа приобретает скорость, направленную противоположно скорости снаряда.
Как найти скорость 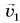
Так как импульс системы до выстрела был равен нулю, то после выстрела:
где 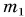
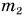
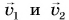
Почему платформа пришла в движение? Потому что пороховые газы, образовавшиеся в канале ствола при выстреле, действовали как на снаряд, так и на пушку. Сила, приложенная к пушке, вызвала движение платформы с пушкой в направлении, противоположном движению снаряда («отдачу»). Аналогичное явление можно наблюдать на простом опыте. Прикрепим к игрушечному автомобилю надутый воздушный шарик (рис. 236). Проколем его в точке А иглой. Образуется струя воздуха, вырывающегося из шарика, и автомобиль приходит в движение. Оно возникло при отделении от тела его части со скоростью, не равной нулю. Его называют реактивным движением, а силу, ускоряющую тело, — реактивной силой.
Реактивная сила возникает при отделении от тела какой-либо его части со скоростью, не равной нулю (относительно тела).
Устройство, создающее реактивную силу, называется реактивным двигателем.
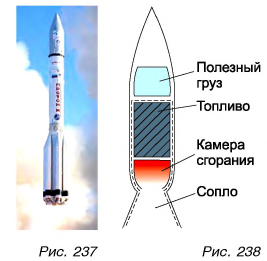
Реактивными двигателями оснащены скоростные самолеты, современные космические корабли (рис. 237). Упрощенная схема реактивного двигателя показана на рисунке 238.
Какую скорость 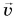
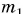
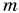
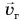
По закону сохранения импульса из формулы (5) находим модуль скорости, приобретаемой ракетой:
Значит, ракета набирает тем большую скорость, чем больше скорость истечения газов из ее сопла и чем меньше масса ракеты. Отсюда понятна выгода использования многоступенчатых ракет (рис. 238). После выгорания топлива в ступени ее отделяют. Масса ракеты уменьшается, что облегчает ее дальнейший разгон. С помощью многоступенчатых ракет выводят на орбиту искусственные спутники Земли, исследуют околоземное и межпланетное космическое пространство.
Первый в мире искусственный спутник Земли был запущен в 1957 г. в СССР. Первый орбитальный полет человека вокруг Земли совершил летчик-космонавт Ю. Гагарин в 1961 г. Американские астронавты Н. Армстронг и Э. Олдрин в 1969 г. первыми высадились на поверхность Луны.
Ракетно-космические исследования стали неотъемлемой частью современной цивилизации. Среди космонавтов есть уроженцы Беларуси: П. И. Климук, В. В. Коваленок, О. В. Новицкий. С космодрома «Байконур» 22 июля 2012 г. был запущен Белорусский космический аппарат (БКА) — спутник массой 400 кг. Он обеспечивает дистанционное зондирование территории Беларуси путем съемки из космоса.
Главные выводы:
- Если результирующая внешних сил равна нулю, то импульс системы сохраняется.
- Закон сохранения импульса можно применить к незамкнутым системам, если влиянием внешних сил можно пренебречь.
- Реактивная сила возникает при отделении от тела какой-либо его части с не равной нулю скоростью.
Пример №2
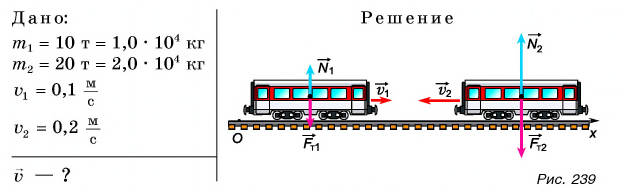
Два вагона массами 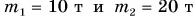
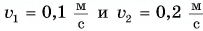
На систему из двух вагонов (рис. 239) действуют внешние силы: силы тяжести 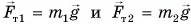
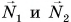
В итоге сумма внешних сил, действующих на вагоны, равна нулю. Значит, к системе из двух вагонов можно применить закон сохранения импульса: 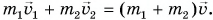
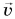
Отсюда
Знак «—» указывает на то, что после автосцепки вагоны будут двигаться противоположно направлению оси Ох.
Ответ: скорость v направлена противоположно оси Ох;
Механическая работа и мощность
В 7-м классе вы познакомились с физической величиной, называемой «механическая работа». Вы узнали, что; в случае когда направление силы F совпадает с направлением движения, работа, которую совершает эта сила, определяется по формуле:
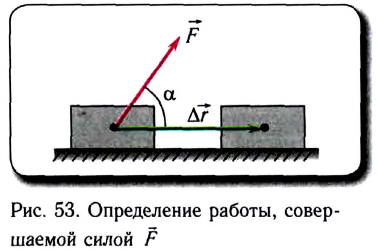
А если сила направлена под углом к перемещению? Как определить работу в этом случае?
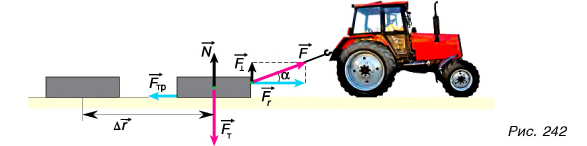
Рассмотрим пример. Трактор передвигает бетонный блок, действуя на него силой 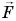
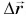
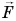
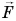
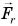
В направлении силы 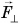
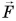
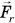
Так как 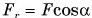
Механическая работа равна модулю силы, умноженному на модуль перемещения и на косинус угла между силой и перемещением.
Работа — скалярная величина.
Единицей работы в СИ является 1 джоуль (1 Дж). Он равен работе, совершаемой силой 1 ныотон при перемещении тела на 1 метр в направлении этой силы (1 Дж = 1 Н • м).
Работа силы может быть положительной, отрицательной или равной нулю. Это зависит от угла между силой и перемещением. Из формулы (1) следует:
- •если угол а острый, то cos а > 0 и работа положительна;
- •если прямой — равна нулю (cosа = 0);
- •если тупой — отрицательна (cos а < 0).
В нашем примере на бетонный блок, кроме силы натяжения троса 
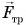
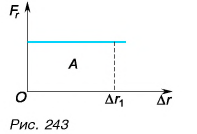
Построим график зависимости проекции силы Fr от модуля перемещения 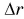
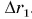
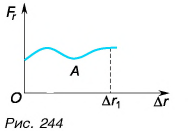
А если сила — переменная величина? В этом случае работа силы также определяется площадью фигуры под графиком зависимости силы Fr от модуля перемещения 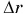
Подсчитаем работу для двух практически важных случаев.
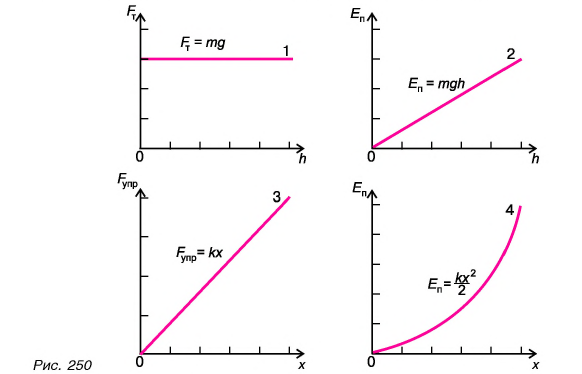
Работа по подъему тела
Тело массой 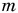
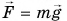
Работа но деформированию пружины
Растянем пружину жесткостью k внешней силой 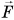
Равенство (3) выполняется и для работы по сжатию пружины.
Для любознательных:
Работа силы зависит от выбора системы отсчета. Рассмотрим пример. Вы находитесь в кабине движущегося лифта. Совершает ли работу действующая на вас сила тяжести? Да, если определять работу этой силы в системе отсчета, связанной с Землей. Нет, если системой отсчета является лифт. Докажите это самостоятельно.
Быстроту совершения работы характеризует мощность. Мощностью называют физическую величину, равную отношению работы к промежутку времени, за который работа совершена:
Мощность численно равна работе, совершаемой за единицу времени. Единицей мощности в СИ является 1 eamm( 1 Вт) — мощность, при которой работа 1 джоуль совершается за 1 секунду. Широко используются кратные единицы мощности: киловатт 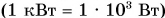
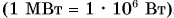
Согласно формуле (4) работа 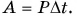
Именно за потребленное количество киловатт-часов (а не киловатт!) электроэнергии мы платим ежемесячно.
Установим связь мощности Р со скоростью движения тела и. Из формул 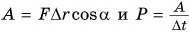
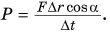
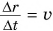
Равенство (5) показывает, что при одной и той же мощности двигателя молено:
- •либо двигаться с большой скоростью при сравнительно малой силе сопротивления движению (рис. 247, а);
- •либо преодолевать большую силу сопротивления, двигаясь с небольшой скоростью (рис. 247, б).
Это используют водители тяжелогруженых машин. При подъеме в гору они уменьшают скорость движения машины, чтобы увеличить силу тяги двигателя.
Главные выводы:
- Работа силы равна произведению модулей силы и перемещения на косинус угла между ними.
- Если угол между силой и перемещением острый, то работа силы положительна, если тупой — отрицательна.
- Силы, перпендикулярные перемещению тела, работу не совершают.
- Мощность численно равна работе, совершаемой за единицу времени.
- Мощность пропорциональна произведению действующей силы и скорости движения тела.
Пример №3
Из колодца глубиной l = 12 м равномерно поднимают ведро воды массой 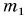
Решение
Учтем, что при подъеме ведра различные точки каната проходят разные пути (от s = 0 для верхней точки каната до s = l для его нижней точки). Тогда работа против сил тяжести, действующих на ведро
где 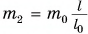
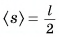
Отсюда
Ответ:
Пример №4
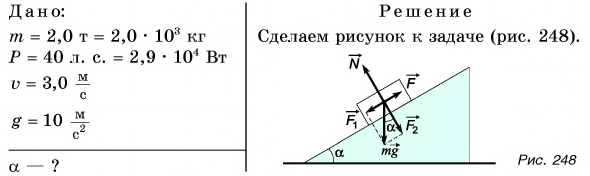
Автомобиль массой m = 2,0 т, развивающий мощность Р = 40 л. c., поднимается в гору с постоянной скоростью, модуль которой 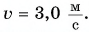
Мощность двигателя 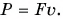
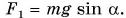
Отсюда
Ответ:
Потенциальная энергия
Вы уже знаете, что и для подъема тела на некоторую высоту, и для его деформации необходимо совершить работу. А какая физическая величина характеризует способность тел совершать работу?
Получим ответ, проведя опыт. О помощью нити и блока соединим гирю массой m с цилиндром немного меньшей массы 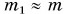
Потенциальная энергия — это мера способности сил взаимодействия механической системы совершать работу. Обозначим потенциальную энергию символом Еп. Она измеряется в тех же единицах, что и работа (в СИ — в джоулях). В дальнейшем мы будем говорить о потенциальной энергии тела, понимая, что речь идет о потенциальной энергии системы взаимодействующих тел.
Как определить потенциальную энергию тела
1. Нужно, прежде всего, определить нулевой уровень, т. е. состояние, в котором потенциальная энергия тела равна нулю. Например, можно принять, что потенциальная энергия гири равна пулю, когда гиря находится на поверхности стола, h = 0 (рис. 249).
2. Затем следует найти работу А, которую совершают силы взаимодействия системы «гиря + Земля» при переходе тела из данного состояния в нулевое (в нашем опыте — при перемещении гири с высоты h на поверхность стола). Эта работа и определяет потенциальную энергию тела:
В нашем опыте работу Л совершала сила тяжести гири 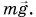
Совпадение выражения 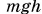
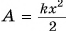
Формула (3) определяет потенциальную энергию любого упругого тела при деформациях сжатия или растяжения.
Для любознательных:
Формулы 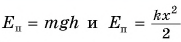
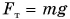
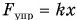
Рассмотрим еще два свойства потенциальной энергии.
1. Изменение потенциальной энергии и работа силы взаимодействия имеют противоположные знаки.
Например, при движении тела массой m вниз с высоты 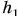
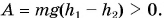
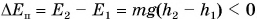
Равенство справедливо для всех видов потенциальной энергии.
2. Нулевой уровень потенциальной энергии можно выбрать произвольно. Значение потенциальной энергии зависит от выбора нулевого уровня. Например (см. рис. 249), если за нулевой уровень принять уровень поверхности пола, а не поверхности стола, то при высоте стола, равной Н, потенциальная энергия гири увеличится на 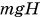
Главные выводы:
- Потенциальная энергия характеризует способность тела совершать работу.
- Потенциальная энергия равна работе силы взаимодействия, совершаемой при переходе тела из данного состояния на нулевой уровень.
- Изменение потенциальной энергии равно работе силы взаимодействия, взятой с противоположным знаком.
Пример №5
Недеформированную пружину жесткостью 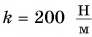
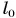
Работа внешней силы: 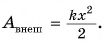
Тогда
Работа силы упругости: 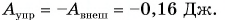
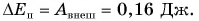
Ответ:
Кинетическая энергия и полная энергия системы тел
Из 7-го класса вы знаете, что, кроме потенциальной энергии, существует и кинетическая. Она зависит от массы и скорости движения тела. А как она связана с работой?
Обратимся к примерам. Молотком забивают в доску гвоздь (рис. 254, а). Движущийся вагон, сталкиваясь с покоящимся, сжимает буферные пружины. Силы, действующие со стороны движущихся молотка, вагона, совершали работу. Значит, движущиеся тела обладают способностью совершать работу. Количественной мерой этой способности является кинетическая энергия (обозначается Ек).
А как тело приобретает кинетическую энергию? В результате работы, произведенной над ним. Например, при метании молота или копья (рис. 254, б) работу совершает мускульная сила спортсмена. Чем больше эта работа, тем сильнее тело разгонится и тем большую кинетическую энергию приобретет.
Кинетическую энергию определяют как величину, равную работе, которую необходимо совершить, чтобы разогнать тело из состояния покоя до данной скорости:
Найдем эту работу. Пусть тело массой т разгоняется из состояния покоя до скорости 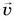
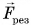
где 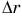
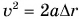
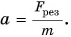
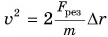
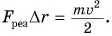
Так как 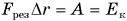
Кинетическая энергия — величина скалярная. Она зависит от модуля скорости, но не зависит от ее направления. Измеряется в тех же единицах, что и работа (в СИ — в джоулях).
А если начальная скорость движения тела 
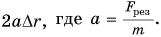
Работа пошла на изменение кинетической энергии тела.
Формула (4) выражает теорему об изменении кинетической энергии.
Изменение кинетической энергии тела равно работе результирующей всех сил, приложенных к нему.
Так как скорость движения относительна, то кинетическая энергия тоже относительна. Например, кинетическая энергия пассажира, сидящего в вагоне движущегося поезда, равна нулю относительно вагона и отлична от нуля относительно платформы. А что такое полная энергия? Чему она равна?
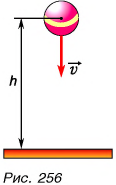
Рассмотрим пример. Пусть падающий мяч массой т в некоторый момент времени находится на высоте h и имеет скорость 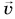
Найдем сумму кинетической и потенциальной энергии мяча. Эту сумму называют механической энергией тела:
Найдена ли полная энергия? Нет.
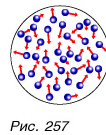
Как вы уже знаете, все тела состоят из микрочастиц — атомов, молекул и др. Эти частицы участвуют в хаотическом тепловом движении (рис. 257) и взаимодействуют (притягивают и отталкивают друг друга). Сумма кинетической энергии теплового движения микрочастиц и потенциальной энергии их взаимодействия друг с другом называется внутренней энергией тела 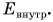
Главные выводы:
- Кинетическая энергия тела прямо пропорциональна его массе и квадрату скорости его движения.
- Значение кинетической энергии зависит от выбора системы отсчета.
- Изменение кинетической энергии равно работе результирующей всех сил, приложенных к телу.
- Механическая энергия тела есть сумма его кинетической и потенциальной энергии.
- Полная энергия тела складывается из его механической и внутренней энергии.
- Заказать решение задач по физике
Пример №6
Камень массой m = 0,50 кг брошен вертикально вверх со скоростью, модуль которой 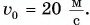
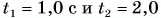
Решение
Найдем модули скорости движения камня 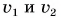
Кинетическая энергия камня через 
Через
Ответ:
Закон сохранения энергии
Полная энергия системы складывается из ее механической энергии и внутренней энергии тел. входящих в систему. При каких условиях механическая и полная энергия системы изменяются? Остаются постоянными?
При подъеме тела возрастает его потенциальная энергия, а при увеличении скорости — кинетическая. А могут ли измениться и кинетическая, и потенциальная энергия одновременно? Рассмотрим пример. Будем поднимать со стола гирю массой m (рис. 258) с помощью прочной нити. Для механической системы «гиря + Земля» сила натяжения нити является внешней силой: 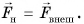
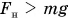
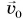
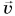
где А — работа результирующей силы 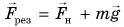
Из равенств (1) и (2) следует:
но 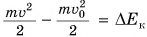
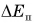
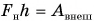
где 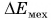
Изменение механической энергии системы, в которой действуют только силы тяжести или упругости, равно работе внешних сил.
Если система замкнута, т. е. на нее не действуют внешние силы, то из равенства (4) следует 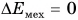
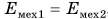
Механическая энергия замкнутой системы, в которой действуют только сила тяжести и силы упругости, остается постоянной (сохраняется). Это утверждение называют законом сохранения механической энергии.
Отметим, что сохраняются не кинетическая и потенциальная энергия по отдельности, а их сумма. В результате в замкнутой системе при уменьшении (увеличении) кинетической энергии настолько же возрастает (уменьшается) потенциальная:
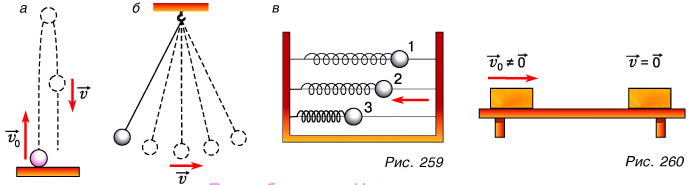
Обсудите, как кинетическая энергия переходит в потенциальную и обратно при движении тел, представленных на рисунке 259.
А что происходит, если система замкнута, но среди ее внутренних сил имеются силы трения и силы сопротивления? Проведем простой опыт. Придадим начальную скорость 
Из-за сил трения потери механической энергии происходят в любом реальном устройстве. Колебания тел, изображенных на рисунке 259, б, в, постепенно затухают, при выключенном двигателе теряет скорость автомобиль и т. д.
Исчезает ли при этом механическая энергия бесследно? При движении бруска по столу происходило нагревание бруска и стола. Только оно было мало, а потому незаметно. При торможении поезда, автомобиля нагреваются тормозные устройства. Под действием сил сопротивления воздуха раскаляются метеориты. При трении друг о друга нагреваются и далее могут плавиться куски льда.
Нагревание происходит и при неупругих деформациях. Согните и разогните несколько раз подряд металлическую проволоку. Вы почувствуете, что в месте сгиба она нагрелась.
Что общего у всех этих явлений? То, что действие сил трения и со противления приводит к увеличению внутренней энергии тел. Хаотическое тепловое движение атомов и молекул становится более быстрым — растет внутренняя кинетическая энергия. Может увеличиться и внутренняя потенциальная энергия (например, при плавлении тел).
Весь накопленный опыт и специально проведенные эксперименты показывают, что в любой замкнутой системе уменьшение механической энергии в точности равно увеличению внутренней, а их сумма (т. е. полная энергия) остается постоянной:
Полная энергия замкнутой системы сохраняется.
Так формулируется один из важнейших законов природы — закон сохранения энергии.
Закон сохранения энергии не знает исключений. Он выполняется для всех физических, химических, биологических и других явлений. Этот закон используется в самых различных областях науки и техники, служит научной основой важнейшей области производства — энергетики.
Добыча энергоносителей (нефти, газа, угля), использование различных источников энергии (воды, ветра, солнечного излучения и т. д.), передача энергии на большие расстояния, борьба с потерями энергии (энергосбережение) являются важнейшими задачами всего мирового сообщества.
Главные выводы:
- Изменение механической энергии системы, в которой действуют силы тяжести и упругости, равно работе внешних сил.
- Полная энергия замкнутой системы сохраняется всегда, а ее механическая энергия сохраняется только при отсутствии сил трения и сопротивления.
- Закон сохранения энергии выполняется для всех явлений природы.
Пример №7
Пакет с цементом массой m = 20 кг поднимают вертикально вверх, прикладывая постоянную силу, модуль которой 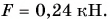
По условию задачи: 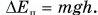
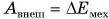
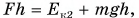
Ответ: 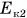
Законы сохранения
Механической системой (от греческого слова 
Силы взаимодействия тел рассматриваемой системы называются внутренними. Силы, действующие на тела рассматриваемой системы со стороны тел, не входящих в нее, называют внешними.
Система называется замкнутой, если тела, ее образующие, взаимодействуют только между собой. В замкнутой системе внешние силы отсутствуют. Систему можно считать замкнутой, если внешними силами можно пренебречь.
Важной динамической характеристикой тела или материальной точки, применяемой для характеристики механического движения, является импульс, или количество движения
Импульс тела
Импульс тела 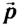
Как следует из определения, направление импульса совпадает с направлением скорости тела, а его единицей в СИ является килограмм на метр в секунду
Запишем второй закон Ньютона в импульсной форме:
Напомним, что в полученном выражении 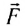
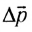
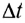
Векторная величина 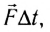
Изменение импульса тела (МТ) относительно инерциальной системы отсчета равно импульсу равнодействующей всех сил, действующих на него.
Таким образом, причиной изменения импульса тела является действие на него сил со стороны других тел. Соответственно, при отсутствии такого действия импульс тела измениться не может — он сохраняет свое значение сколь угодно долго. В этом случае
Подчеркнем, что основной закон динамики, записанный в импульсной форме, носит более общий характер, поскольку он справедлив и в том случае, когда масса тела при движении изменяется. Кроме того, в такой форме записи второй закон Ньютона справедлив и в релятивистской динамике, т. е. при движении со скоростями, сравнимыми со скоростью света в вакууме.
При рассмотрении незамкнутой механической системы тел необходимо учитывать, что каждое из тел системы может взаимодействовать как с телами этой системы, так и с телами, не входящими в нее.
Поскольку согласно третьему закону Ньютона внутренние силы в системе возникают парами и при суммировании компенсируют друг друга, то их вклад в равнодействующую равен нулю. Следовательно, изменение импульса механической системы в целом может происходить только под действием внешних сил, приложенных к ней.
При действии нескольких внешних сил 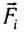
где 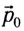
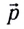
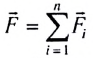
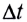
Изменение импульса незамкнутой механической системы относительно инерциальной системы отсчета равно импульсу равнодействующей всех внешних сил, действующих на нее.
Если результирующая внешняя сила, действующая на механическую систему, равна нулю 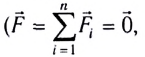
Таким образом, для замкнутых механических систем выполняется закон сохранения импульса:
- векторная сумма импульсов тел в замкнутой механической системе остается постоянной при любых взаимодействиях тел системы между собой.
Поскольку число взаимодействующих объектов во Вселенной велико, то, строго говоря, замкнутая система — это идеализация. Однако в случае кратковременного взаимодействия (столкновение, удар, взрыв), при котором 
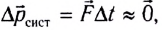
В случае, когда система незамкнута, но сумма проекций сил на какую-либо ось равна нулю, система называется частично замкнутой или замкнутой на данную ось. Например, если проекция равнодействующей на ось Оу равна нулю 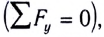
Реактивное движение
Закон сохранения импульса позволяет объяснить возникновение реактивного движения, широко используемого в науке и технике, например при космических полетах. Его также можно наблюдать в живой природе.
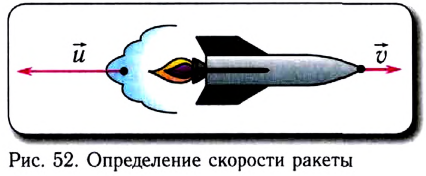
Рассмотрим простейшую ракету как систему двух взаимодействующих тел (рис. 51), одно из которых представляет собой замкнутую оболочку (трубку) с соплом, а второе — содержащуюся внутри ракеты горючую смесь (топливо).
При горении смеси раскаленные газы с большой скоростью выбрасываются из ракеты. Оболочка при этом разгоняется в противоположную сторону в соответствии с законом сохранения импульса. После выгорания топлива ракета, подобно брошенному камню, совершает свой дальнейший полет по баллистической траектории.
До начала работы двигателей сумма импульсов ракеты 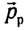
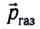
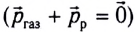
где М — масса ракеты, 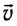
Отсюда получаем
Отметим, что эта формула справедлива при условии незначительного изменения массы М ракеты в результате работы ее двигателей.
Из второго закона Ньютона, записанного в импульсной форме
следует, что изменение импульса тела, связанное с действием силы, может возникать не только при изменении скорости тела, но и при изменении его массы.
Законы движения тел с переменной массой (ракет) были исследованы русскими учеными И. В. Мещерским и К. Э. Циолковским.
Циолковский одним из первых обосновал идею космических полетов с помощью ракет и выхода человека в космос, а также получил широко известную формулу, связывающую массу ракеты с ее скоростью.
Уравнение Мещерского позволяет определить реактивную силу, действующую на ракету со стороны реактивной струи газов.
Пусть в данной ИСО в некоторый момент времени t скорость ракеты равна 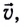
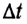
где 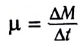
За это время скорость ракеты увеличится до значения 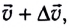
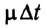
Из закона сохранения импульса
Раскрывая скобки и пренебрегая членом, содержащим произведение двух малых величин 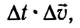
где 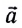
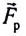
Таким образом, реактивная сила тяги, действующая на ракету, определяется скоростью истечения газов 
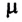
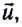
Особенностью реактивного движения является тот факт, что оно может быть реализовано как в земных, так и в космических условиях, поскольку реактивная сила тяги практически не зависит от свойств окружающей среды и от скорости движения объекта. Это обстоятельство обеспечило широкое распространение
реактивных двигателей при создании современных высокоскоростных судов, самолетов, космических ракет.
Работа и мощность в механике
Работа — скалярная физическая величина, прямо пропорциональная модулю силы F, совершающей работу, и пройденному пути s: A=Fs, если направление силы совпадает с направлением движения.
При динамическом подходе к описанию механического движения определяющим понятием является импульс силы, зависящий от времени ее воздействия.
Для описания действия силы при перемещении тела на определенное расстояние вводится скалярная физическая величина, называемая работой силы.
Если под действием силы 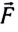
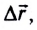
Работа — скалярная физическая величина, равная произведению модуля силы F, модуля перемещения 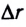
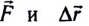
Данное определение справедливо для постоянной (как по модулю, так и по направлению) силы 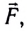
В СИ единицей работы является джоуль (1 Дж= 1 Н • 1 м).
Один джоуль — это работа, которую совершает сила в один ньютон, действующая на тело в направлении его перемещения, на пути в один метр.
Если графически изобразить зависимость проекции силы 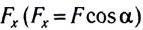
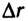
Рассмотрим некоторые наиболее распространенные случаи вычисления работы: 1.Если угол между направлением силы, совершающей работу, и перемещением равен нулю (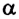
Так, сила тяги, создаваемая двигателем автомобиля, совершает положительную работу при его разгоне.
2. Если угол между направлением силы и перемещением 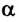
А = 0. (3)
Так, при вращении шарика на нити сила натяжения нити не совершает работу и модуль скорости шарика не меняется.
3. Если угол между направлением силы и перемещением 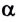
Так, сила сопротивления среды совершает отрицательную работу, что при выключенном двигателе автомобиля приводит к уменьшению его скорости до полной его остановки.
Во многих случаях в процессе движения сила меняется и по модулю, и по направлению, т. е. не выполняются условия, при которых справедлива формула для работы (1). Тогда для нахождения работы необходимо весь путь разделить на такие малые участки 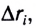
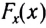
Существует два класса сил — потенциальные (консервативные) и непотенциальные (неконсервативные).
Если работа силы не зависит от траектории движения тела, а определяется только его начальным и конечным положениями в пространстве, то сила является потенциальной. Следует подчеркнуть, что модуль потенциальных сил определяется только расположением тел в пространстве, т. е. расстояниями между взаимодействующими телами.
Можно показать, что работа потенциальной силы при перемещении тела по любой замкнутой траектории всегда равна нулю.
Заметим, что если на каком-либо участке пути потенциальные силы совершают некоторую работу А над телом, то при движении по той же траектории в обратном направлении будет совершена работа — А.
Потенциальными являются силы упругости, силы гравитационного притяжения, сила тяжести.
Если работа силы зависит от траектории движения тела, то говорят о непотенциальной силе, примером которой является сила трения. Действительно, работа силы трения отрицательна при перемещении тела по участку траектории, как в прямом, так и в обратном направлении.
Величину работы, совершаемой постоянной силой 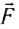
Мощность Р — скалярная физическая величина, определяющая быстроту совершения работы.
Единицей мощности в СИ является ватт
Средняя мощность равна отношению совершенной работы А к промежутку времени 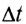
С учетом того, что 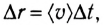
Следовательно, мгновенную мощность Р можно определить по формуле:
Таким образом, мгновенная мощность силы равна произведению модуля силы, модуля скорости тела и косинуса угла 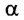
Подчеркнем, что полученная формула справедлива и в случае изменяющихся с течением времени значений силы и скорости.
Кинетическая и потенциальная энергии. Закон сохранения энергии в механике
Кинетическая энергия тела — скалярная физическая величина, равная работе, совершенной при разгоне данного тела из состояния покоя до данной скорости, или величина, равная работе силы, необходимой для остановки данного тела. Потенциальная энергия — это энергия, обусловленная расположением взаимодействующих тел или частей тела.
Работа силы связана с изменением механической энергии при переходе системы из одного состояния в другое. Энергия — это скалярная физическая величина, характеризующая способность тела или системы тел совершать работу. Изменение энергии системы определяется работой, совершенной внешними силами, приложенными к системе.
Термин «энергия» был введен В. Дж. Ренкиным в 1853 г. при рассмотрении закона сохранения энергии в немеханических системах. Он образован от греческого слова 
В механике состояние системы определено, если известно положение тел системы (их координаты) и импульсы всех тел системы. В соответствии с этим в механике существуют два вида энергии — потенциальная и кинетическая.
Кинетическая энергия (энергия движения) — вид механической энергии, которой обладают тела вследствие их движения. Кинетическая энергия движущегося тела в заданной ИСО равна работе, которую нужно совершить для полной остановки тела.
Рассмотрим тело, движущееся со скоростью 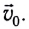
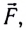
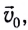
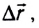
Вследствие того, что конечная скорость тела v = 0, получаем
Таким образом, при поступательном движении твердого тела его кинетическая энергия определяется по формуле
где m — масса тела, v — скорость любой точки тела (например, центра тяжести).
Отметим, что эта формула верна лишь для скоростей движения V, намного меньших скорости света с, т. е. при
Теорема о кинетической энергии:
изменение кинетической энергии 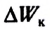
где 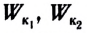
Потенциальная энергия
Потенциальная энергия (энергия положения) — вид механической энергии, обусловленной взаимодействием тел или частей одного и того же тела и зависящей только от координат тел.
Потенциальная энергия системы взаимодействующих тел — это физическая величина, численно равная работе, совершаемой силами взаимодействия при взаимном удалении всех тел системы из данного положения на бесконечное расстояние друг от друга. В этом положении потенциальная энергия считается равной нулю.
На тело, находящееся у поверхности Земли, действует сила тяжести. Для изменения положения тела над поверхностью Земли сила тяжести 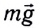
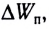
Такой выбор знака приводит к тому, что работа силы тяжести положительна при движении тела вниз, а значит, потенциальная энергия 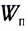
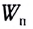
В однородном поле силы тяжести (вблизи поверхности Земли) потенциальной энергией 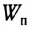
где h — высота над уровнем, условно принятым за нулевой. Отметим, что эта высота должна быть намного меньше радиуса R планеты, т. е.
Выбор состояния, энергия которого принимается за нулевой уровень, совершенно произволен и определяется только соображениями удобства.
Потенциальная энергия упруго деформированного тела определяется работой, которую совершают силы упругости, возвращая тело в недеформированное состояние. Модуль силы упругости 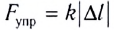
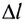
Потенциальной энергией упруго деформированного тела является величина
где k — жесткость образца, 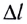
Единицей энергии, как и работы, в СИ является джоуль (1 Дж).
Сумма кинетической и потенциальной энергий называется полной механической энергией системы:
Таким образом, в общем случае работа А, совершенная над системой тел, равна приращению ее энергии
Если механическая система является консервативной, т. е. если внешние и внутренние силы, действующие на тела системы, являются потенциальными и работа внешних сил равна нулю, то
Следовательно,
т. е. механическая энергия системы сохраняется.
Для таких систем выполняется закон сохранения механической энергии: полная механическая энергия консервативной физической системы является величиной постоянной:
Закон сохранения механической энергии справедлив и для незамкнутых систем в том случае, если внешнее силовое ноле потенциально и стационарно.
Закон сохранения механической энергии является частным случаем закона сохранения и превращения энергии:
при любых процессах энергия не увеличивается и не уменьшается. Энергия может превращаться из одного вида в другой и передаваться от одного тела другому, но ее полная величина сохраняется постоянной.
Границы применения физических законов и теорий
Физики установили существование четырех видов взаимодействия между частицами: сильное, электромагнитное, слабое и гравитационное (отмечено в порядке уменьшения интенсивности). Современные теории всех взаимодействий являются квантовыми.
Интенсивность любого взаимодействия принято характеризовать с помощью так называемого постоянного взаимодействия, которое определяет вероятность процессов, обусловленных данным видом взаимодействия. Отношение значений констант показывает относительную интенсивность соответствующих взаимодействий, которая дает возможность сравнить их.
Самым универсальным среди взаимодействий является гравитационное -оно возникает между любыми телами, имеющими массу.
В физике частиц гравитационное взаимодействие не имеет никакого значения на расстояниях больше 10-35 м. При меньших расстояниях или очень больших энергиях это взаимодействие по значению сравнивается с другими взаимодействиями.
Электромагнитное взаимодействие возникает между телами, имеющими электрический заряд.
Слабое и сильное взаимодействия — ядерные. Слабое взаимодействие руководит распадом тяжелых частиц на более легкие и изменяет внутреннюю природу частиц. Сильное взаимодействие — это взаимодействие между кварками, которое и обусловливает ядерное взаимодействие, а также разные ядерные реакции. Это взаимодействие почти в 1037 раз сильнее гравитационного.
Каждому фундаментальному взаимодействию соответствует своя частица, переносящая это взаимодействие. Для гравитации — это гравитоны, для электромагнитного взаимодействия — фотоны, сильное взаимодействие обусловливается глюонами, слабое — векторными бозонами.
Как же осуществляются эти взаимодействия?
Электромагнитное взаимодействие: переносчик — фотон. Гравитационное взаимодействие: переносчики — кванты поля тяготения — гравитоны. И фотоны, и гравитоны не имеют массы (массы покоя) и всегда движутся со скоростью света. Слабые взаимодействия: переносчики — векторные бозоны. Существенным отличием переносчиков слабого взаимодействия от фотона и гравитона является их массивность. Переносчики сильных взаимодействий — глюоны (англ, glue — «клей») с массой покоя, равной нулю.
Ряд существенных открытий, сделанных в фундаментальной физике, особенно в физике высоких энергий, важные экспериментальные результаты открывают глубокую взаимосвязь частиц и скрытых сил, действующих внутри вещества. Ученые выдвинули гипотезу, согласно которой вся природа подчинена действию некоей суперсилы, являющейся достаточно мощной, чтобы создать нашу Вселенную и наделить ее светом, энергией, материей и предоставить ей структуру. В суперсиле материя, пространство-время и взаимодействие слиты в неразделимое гармоничное целое, порождающее такое единство Вселенной, которого раньше никто и не предполагал.
Фундаментальные законы достаточно абстрактно сформулированы, и не являются следствием экспериментов. Обычно фундаментальные законы «угадываются», а не выводятся из эмпирических. Количество таких законов очень ограничено (например, классическая механика имеет лишь четыре фундаментальных закона: три закона Ньютона и закон всемирного тяготения). Многочисленные эмпирические законы являются последствиями (иногда вовсе не очевидными) фундаментальных. Критерием истинности последних является соответствие конкретных последствий экспериментальным наблюдениям. Все известные сегодня фундаментальные законы описываются достаточно простыми математическими выражениями. Границы применения фундаментальных законов ограничены. Эта ограниченность не связана с математическими неточностями, а имеет более фундаментальный характер: при выходе за границы
применения фундаментального закона начинают терять смысл сами понятия, используемые в формулировках. Так, для микрообъектов оказывается невозможным строгое определение понятий ускорения и силы, которая ограничивает применение законов Ньютона.
Ограниченность применения фундаментальных законов естественно приводит к вопросу о существовании еще более общих законов. Такими являются законы сохранения. Существующий опыт развития естествознания показывает, что законы сохранения не теряют своего смысла при замене одной системы фундаментальных законов другой. В большинстве случаев законы сохранения не способны дать такого полного описания явлений, которое дают фундаментальные законы, а лишь накладывают определенные запреты на реализацию тех или иных состояний при эволюции системы.
Мы уже говорили, что первый закон Ньютона выполняется только в инерциальных системах отсчета. Второй закон также выполняется лишь в инерциальных системах. Третий закон выполняется и в неинерциальных системах, но не всегда. Он не выполняется для так называемых сил инерции. Следовательно, первым ограничением законов Ньютона является то, что они выполняются только в инерциальных системах отсчета.
Механика Ньютона является механикой малых скоростей (сравнительно со скоростью распространения света). Движение в микромире (мире молекул, атомов и элементарных частиц) подчиняется другим законам. Поэтому механика Ньютона неприменима к микромиру, она является механикой больших тел (конечно, сравнимых с размерами молекул).
Следовательно, классическая механика Галилея-Ньютона выполняется лишь в инерциальных системах для больших тел, движущихся с малыми скоростями, а потому считать ее универсальной нельзя.
Каждый физический закон имеет свои границы применения. Это, в первую очередь, касается закона сохранения механической энергии. Первое важное ограничение данного закона — система рассматриваемых тел должна быть изолирована от внешних влияний. Такую систему называют замкнутой. Второе ограничение связано с тем, что не всегда работа однозначно определяется изменением потенциальной энергии тела при перемещении его с одной точки поля в другую. Однозначное определение работы как меры изменения потенциальной энергии имеет место лишь для определенных типов полей, которые называют потенциальными. Примерами таких полей является гравитационное или электростатическое поле. Потенциальными считаются поля, работа сил которых не зависит от траектории движения тела в поле. Соответственно, силы этих полей называют консервативными. Если работа сил зависит от формы пути или силы зависят от скорости движения, то механическая энергия системы не сохраняется. Например, силы трения, не являющиеся консервативными, присутствуют во всех случаях. Следовательно, закон сохранения механической энергии выполняется лишь для идеализированных ситуаций.
Изучая закон Гука, следует помнить, что он имеет определенные границы применения или границы, в которых он выполняется, а именно «предел упругости».
Закон Ома также имеет границы применения, хотя и достаточно широкие — вплоть до чрезвычайно малых токов. Закон Ома не выполняется в тех случаях, когда ток очень слабый (или очень большой), и начинают проявляться флуктуации числа носителей тока — электронов в металле. Тогда закон, имеющий принципиально статистический характер, не выполняется.
Законы прямолинейного распространения света, отражения и преломления выполняются лишь при определенных условиях, когда длина световых волн намного меньше размеров отверстий и экранов, с которыми взаимодействует свет при распространении.
Фундаментальный характер законов сохранения в природе
Фундаментальные физические законы — самое полное, но приближенное отражение объективных процессов в природе. Разные формы движения материи описываются разными фундаментальными теориями. Каждая из этих теорий описывает полностью определенные явления: механическое или тепловое движение, электромагнитные явления.
Законы сохранения — утверждения, согласно которым числовые значения этих величин не меняются со временем в любых процессах.
Идея сохранения появилась сначала как сугубо философская точка зрения о наличии неизменного, стабильного в вечно переменчивом мире. Еще античные философы-материалисты пришли к понятию материи как неуничтожимой и несоздаваемой. С другой стороны, наблюдение постоянных изменений в природе приводило к представлению о вечном движении материи как важном ее свойстве. С появлением материалистической формулировки механики на этой основе появились законы сохранения.
Самыми важными законами сохранения, которые выполняются для любых изолированных систем, являются закон сохранения энергии и закон сохранения импульса.
Закон сохранения энергии в механических процессах. Механическая энергия разделяется на два вида: потенциальную (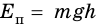
поднято на определенную высоту над Землей, 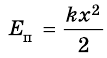
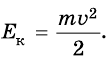
Рассмотрим теперь вопрос об изменении энергии при взаимодействии тел, образующих замкнутую систему. Если несколько тел взаимодействуют между собой лишь силами тяготения и силами упругости и никакие внешние силы не действуют, то при любых взаимодействиях сумма кинетической и потенциальной энергий тел остается постоянной. Это утверждение называют законом сохранения энергии в механических процессах.
Сумму кинетической и потенциальной энергий тел называют полной механической энергией 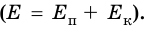
Закон сохранения полной механической энергии в процессах при участии сил упругости и гравитационных сил является одним из основных законов механики. Знание данного закона упрощает решение многих задач, имеющих практическое значение. Например, для получения электроэнергии широко используют энергию рек. С этой целью строят плотины, перегораживают реки. Под действием сил притяжения вода из водохранилища по плотине движется вниз ускоренно и приобретает определенную кинетическую энергию. При столкновении потока воды с лопатками гидравлической турбины происходит превращение кинетической энергии поступательного движения воды в кинетическую энергию вращательного движения роторов турбины, а потом с помощью электрического генератора — в электрическую энергию.
Механическая энергия не сохраняется, если между телами действует сила трения. Автомобиль, движущийся по горизонтальному участку дороги, после выключения двигателя проходит определенный путь и под действием сил трения останавливается. При торможении автомобиля происходит нагревание тормозных колодок, шин автомобиля, асфальта. В результате действия сил трения кинетическая энергия автомобиля не исчезла, а превратилась во внутреннюю энергию теплового движения молекул. Следовательно, при любых физических взаимодействиях энергия не возникает, а только превращается из одного вида в другой. Этот экспериментально установленный факт называют законом сохранения и превращения энергии. Источники энергии на Земле большие и разнообразные. В давние времена люди знали только один источник энергии — силу мышц и силу домашних животных. Энергия возобновлялась за счет потребления еды.
Энергия окружающего космического пространства аккумулируется Солнцем в виде энергии атомных ядер, химических элементов, электромагнитных и гравитационных полей. Солнце, в свою очередь, обеспечивает Землю энергией в виде энергии ветра и волн, приливов и отливов, в форме геомагнетизма, разного вида излучений, энергии мышц животного мира.
Геофизическая энергия высвобождается в виде природных стихийных явлений, обмена веществ в живых организмах, полезной работы по перемещению тел, изменения их структуры, качества, передачи информации, запаса энергии в разного рода аккумуляторах, в упругой деформации пружин, мембран.
Любые виды энергии, превращаясь друг в друга с помощью механического движения, химических реакций и электромагнитных излучений, в конце концов, переходят в тепло и рассеиваются в окружающем пространстве. Это явление проявляется в виде взрывных процессов, горения, гниения, плавления, испарения, деформации, радиоактивного распада.
Происходит кругооборот энергии в природе, который характеризуется не только хаотичностью, но и обратным ей процессом — упорядочиванием структуры, которые наглядно прослеживаются, в первую очередь, в звездообразовании, трансформации и возникновении новых электромагнитных и гравитационных полей, и они опять несут свою энергию новым «солнечным системам».
Закон сохранения механической энергии сформулировал немецкий ученый Готфрид Лейбниц. Потом немецкий ученый Юлиус Майер, английский физик Джеймс Джоуль и немецкий ученый Генрих Гельмгольц экспериментально открыли законы сохранения энергии в немеханических явлениях.
Закон сохранения импульса
Покой и движение тела относительны, скорость движения зависит от выбора системы отсчета. Согласно второму закону Ньютона, независимо от того, находится ли тело в покое или движется равномерно и прямолинейно, изменение его скорости движения может происходить только под действием силы, то есть в результате взаимодействия с другими телами.
Есть физическая величина, которая одинаково изменяется у всех тел под действием одинаковых сил. Она определяется произведением массы тела и его скорости и называется импульсом тела. Импульс тела — величина векторная, сонаправленная со скоростью движения тела. Импульс тела является количественной характеристикой поступательного движения тел. Экспериментальные исследования взаимодействия разных тел — от планет и звезд до атомов и электронов, элементарных частиц — показали, что в любой системе взаимодействующих между собой тел геометрическая сумма импульсов этих тел остается постоянной: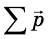
Систему тел, невзаимодействующих с другими телами, невходящими в эту систему, называют замкнутой. Таким образом, в замкнутой системе геометрическая сумма импульсов тел остается постоянной при любых взаимодействиях тел этой системы между собой. Этот фундаментальный закон природы называют законом сохранения импульса.
Необходимым условием применения закона сохранения импульса к системе взаимодействующих тел является использование инерциальной системы отсчета. На законе сохранение импульса основывается реактивное движение, его используют при расчете направленных взрывов, например при прокладке тоннелей в горах. Полеты в космос стали возможными благодаря использованию многоступенчатых ракет.
- Международная система единиц СИ
- Математика — язык физики
- Законы Ньютона в физике
- Гравитационные силы в физике
- Ядерная энергетика в физике
- Динамика в физике
- Статика в физике
- Кинематика в физике
Законы, сформулированных Ньютоном, позволяют решить различные практически важные задачи, касающиеся взаимодействия и движения тел. Большое число таких задач связано, например, с нахождением ускорения движущегося тела, если известны все действующие на это тело силы. А далее по ускорению можно определить и другие величины, такие как перемещение, мгновенную скорость и др.
Прежде чем сформулировать закон сохранения импульса, давайте введем понятие импульса и проследим, каким образом связано это понятие с законами Ньютона, с которыми мы познакомились ранее.
Основным законом динамики, как мы уже говорили, является второй закон Ньютона, связывающий ускорение тела с его массой m и силой
, действующей на это тело:
Зная связь ускорения тела со скоростью его движения и предполагая, что масса тела не изменяется с течением времени, выражение можно переписать несколько в ином виде:
|
|
Полученное выражение показывает, что результат действия силы можно понимать и несколько иначе, чем мы делали это раньше: действие силы на тело приводит к изменению некоторой величины, характеризующей это тело, которая равна произведению массы тела на скорость его движения. Эту величину называют импульсом тела :
|
|
Направление вектора импульса тела всегда совпадает с направлением вектора скорости движения.
Слово «импульс» в переводе с латинского означает «толчок». В некоторых книгах вместо термина «импульс» используется термин «количество движения».
Эта величина была введена в науку примерно в тот же период времени, когда Ньютоном были открыты законы, названные впоследствии его именем. Ещё в первой половине XVII века понятие импульса введено Рене Декартом. Так как физическое понятие массы в то время отсутствовало, он определил импульс как произведение «величины тела на скорость его движения». Позже такое определение было уточнено Исааком Ньютоном. Согласно Ньютону, «количество движения есть мера такового, устанавливаемая пропорционально скорости и массе».
Поскольку 
При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу. Если на систему тел не действуют внешние силы со стороны других тел, то такая система называется замкнутой.
В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.
Этот фундаментальный закон природы называется законом сохранения импульса. Он является следствием из второго и третьего законов Ньютона.
Рассмотрим какие-либо два взаимодействующих тела, входящих в состав замкнутой системы. Силы взаимодействия между этими телами обозначим через 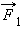
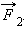
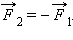
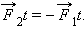
где 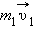
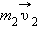
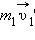
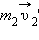
Это равенство означает, что в результате взаимодействия двух тел их суммарный импульс не изменился. Рассматривая теперь всевозможные парные взаимодействия тел, входящих в замкнутую систему, можно сделать вывод, что внутренние силы замкнутой системы не могут изменить ее суммарный импульс, т. е. векторную сумму импульсов всех тел, входящих в эту систему.
Закон сохранения импульса во многих случаях позволяет находить скорости взаимодействующих тел даже тогда, когда значения действующих сил неизвестны. Примером может служить реактивное движение.
При стрельбе из орудия возникает отдача – снаряд движется вперед, а пушка– откатывается назад. Снаряд и пушка – два взаимодействующих тела. Скорость, которую приобретает пушка при отдаче, зависит только от скорости снаряда и отношения масс. Если скорости пушки и снаряда обозначить через 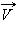
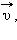
Если тело покоится, импульс равен нулю. Ненулевым импульсом обладает любое, движущееся тело. Например, когда мяч покоится, его импульс равен нулю. После удара он приобретает импульс. Импульс тела изменяется, так как изменяется скорость.
Рассмотрим задачу, которая демонстрирует связь импульса силы и изменения импульса тела.
Пример. Масса мяча равна 400 г, скорость, которую приобрел мяч после удара — 30 м/с. Сила, с которой нога действовала на мяч — 1500 Н, а время удара 8 мс. Найти импульс силы и изменение импульса тела для мяча.
Изменение импульса тела:
Как определить изменение импульса тела? Необходимо найти численное значение импульса в один момент времени, затем импульс через промежуток времени. От второй найденной величины отнять первую. Внимание! Вычитать надо вектора, а не числа. То есть из второго вектора импульса отнять первый вектор. Смотрите вычитание векторов.
Пример. Оценить среднюю силу со стороны пола, действующую на мяч во время удара.
1) Во время удара на мяч действуют две силы: сила реакции опоры, сила тяжести.
Сила реакции изменяется в течение времени удара, поэтому возможно найти среднюю силу реакции пола.
2) Изменение импульса 
3) Из второго закона Ньютона
Главное запомнить
1) Формулы импульса тела, импульса силы;
2) Направление вектора импульса;
3) Находить изменение импульса тела







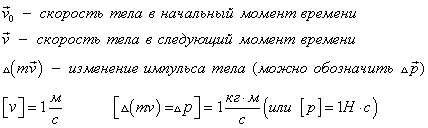




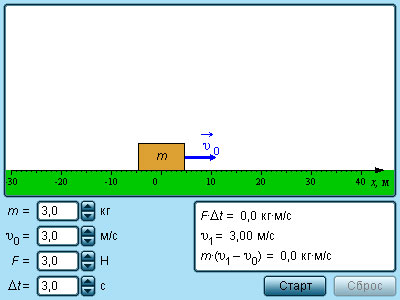
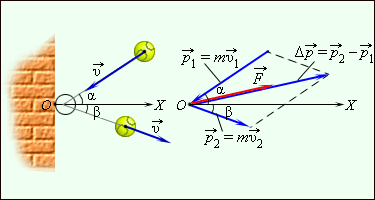





























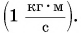
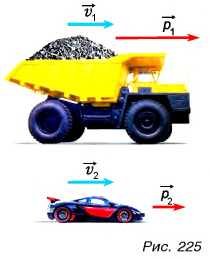
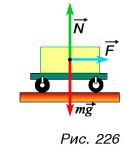
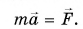

 направлено так же, как результирующая сила F;
направлено так же, как результирующая сила F;