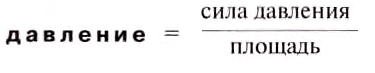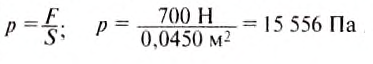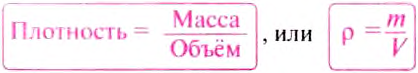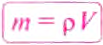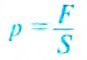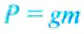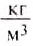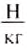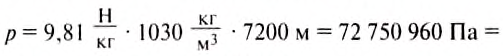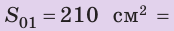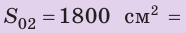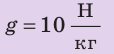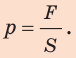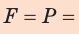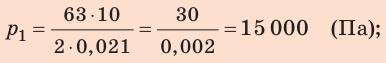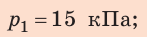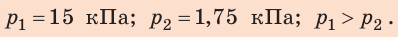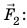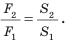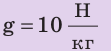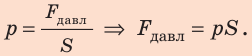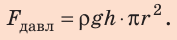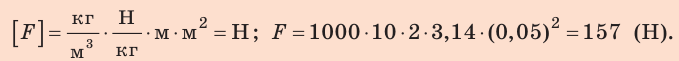Способы
уменьшения и увеличения давления
«Ох,
нелегкая это работа –
вездеходы
катать по болотам»
Дмитрий Зыков
В
данной теме речь пойдёт о практической пользе уменьшения или увеличения
давления.
Давление
– это отношение силы, действующей перпендикулярно поверхности, к площади этой
поверхности. Давление измеряется в Н/м2. Такая
единица была названа Па (паскалем) в честь ученого Блеза Паскаля. Таким
образом, давление в 1 Па – это давление, которое производит сила в 1 Н,
действующая на поверхность площадью 1 м2.
Возникает
вопрос о том, как можно контролировать (то есть, увеличивать, или уменьшать)
давление? На этот вопрос нетрудно ответить, если посмотреть на формулу, по
которой вычисляется давление.
Для
увеличения давления необходимо либо увеличить силу, либо уменьшить площадь.
И, наоборот, для уменьшения давления нужно либо уменьшить силу, либо
увеличить площадь.
В
этом можно убедиться на ряде примеров. Если идти по снегу на лыжах, то человек
не проваливается, хотя без лыж, его ноги будут утопать в снегу. В этом случае,
сила, действующая на поверхность (то есть вес), остается неизменной. Но вот
площадь лыж значительно больше ступни, поэтому в лыжах человек оказывает на
снег меньшее давление, чем без лыж. Люди используют уменьшение или
увеличение давления очень часто. Шины грузовых автомобилей значительно шире,
чем шины легковых автомобилей. Это делается не только для большей устойчивости,
но и для уменьшения давления. В особенности это важно для автомобилей,
предназначенных для езды в пустыне или по бездорожью.
Даже
такие тяжелые машины, как танк или трактор не оказывают на почву значительно
большее давление, чем взрослый человек. Дело в том, что площадь гусеницы
танка во много раз превышает площадь ступни человека. Таким образом, танк
нередко может пройти по той болотистой местности, по которой не пройдет
человек.
Передвигаясь
в подобного рода местностях, люди нередко используют так называемые мокроступы.
За
счет увеличения площади, эта обувь из пластика или резины позволяет передвигаться
по заболоченным местностям, не проваливаясь в грязь и трясину. Раньше
мокроступы изготавливались из древесины наподобие лаптей. Во время Великой
Отечественной Войны, такие мокроступы были использованы в ходе проведения
знаменитой операции «Багратион». Совершенно неожиданно для немецкого
командования, несколько советских армий и корпусов ударили в тыл немецкой
группы армий «Центр», пройдя через болота, которые немцы считали непроходимыми.
В результате этой крупномасштабной операции было завершено освобождение
Белоруссии, и советские войска вошли в Польшу.
Также
нередко возникает необходимость в увеличении давления. Это, как правило,
нужно для колющих и режущих инструментов, таких, как ножи, ножницы, бритвы и
так далее. Острые лезвия имеют очень маленькую площадь поверхности,
поэтому, даже небольшим усилием можно создать большое давление. Например, играя
в дартс, игроки бросают дротики с небольшой силой, но при попадании в мишень
они создают давление, которое может в несколько десятков раз превышать давление
гусеничного трактора на почву.
Подобные
примеры нередко встречаются и в природе – это зубы, когти или клювы животных.
За
счет того, что они имеют малую площадь поверхности и способны развивать
значительное усилие, создается огромное давление. Например, оса
действует своим жалом на кожу человека с силой всего в 10 мкН. Однако
площадь жала осы настолько мала, что и это усилие создает давление в
миллиарды паскалей.
Давление
также учитывается в строительстве. Например, при возведении
зданий, увеличивают площадь нижней части фундамента, чтобы грунт мог
выдержать давление, создаваемое зданием. При строительстве мостов, нагрузку
также стараются распределить, делая больше опор.
Приведем
еще пару интересных примеров. Известно, что давление под водой увеличивается по
мере погружения на большую глубину. Это происходит из-за увеличения силы
давления воды, поскольку чем глубже погружаться, тем большее
количество воды давит на аквалангиста, то есть, увеличивается сила
давления. Именно по этой причине, различные подводные обитатели не могут
опускаться ниже определенных глубин (или, наоборот, подниматься выше
определенных глубин).
Упражнения.
Задача
1.
Если человек и гусеничный трактор оказывают одинаковое давление на почву, то
почему трактор, наехав на кирпич, сломает его, а человек, встав на кирпич, не
повредит ему?
Решение:
Человек
и трактор давят на почву одинаково.
pт = pч
Это
происходит, потому что отношение веса трактора к площади его гусениц равно
отношению веса человека к площади его ступней.
PТ / SГ = PЧ / SС
Однако
когда трактор наезжает на кирпич, следует брать в расчет не площадь гусениц
трактора, а площадь кирпича, на которую трактор действует всем своим весом.
Естественно, при этом развивается многократно большее давление, чем под
действием веса человека. Если же выложить трактору полосу из кирпичей, то его
вес распределится равномерно по нескольким кирпичам и давление уменьшится.
pт ≠ pч
PТ / SГ ≠ PЧ / SС
Задача
2.
На обочине стоит припаркованный автомобиль. Площадь части шины, соприкасающейся
с дорожным покрытием, равна 0,07 м2. Рядом стоит точно такой же
автомобиль, с более широкими шинами, так что площадь части шины, соприкасающейся
с дорожным покрытием, равна 0,077 м2. Во сколько раз давление,
оказываемое первым автомобилем на почву, больше, чем давление, оказываемое
вторым автомобилем?
Основные
выводы:
–
Давление – это физическая величина, равная отношению силы, действующей
перпендикулярно поверхности, к площади этой поверхности.
–
Для увеличения давления на опору, необходимо либо увеличить силу, либо
уменьшить площадь опоры.
–
Для уменьшения давления на опору, необходимо, либо уменьшить силу, либо
увеличить площадь опоры.
–
Уменьшение и увеличение давления часто используется людьми на практике.
Содержание:
Сила давления и единицы давления:
Вы уже знаете, что действие одного тела на другое характеризуют приложенной к нему силой. От чего зависит результат действия этой силы на тело?
Наблюдение 1. Из собственного опыта вы знаете, что очень тяжело идти по глубокому рыхлому снегу, поскольку ноги глубоко проваливаются в нём, а на лыжах передвигаться намного легче, так как проседание снеговой поверхности в этому случае значительно меньше. В обоих случаях вы действуете на снег с одинаковой силой, но площадь поверхности, на которую она распределяется в случае лыж значительно больше, чем в случае обуви, поэтому и деформация снега оказывается разной. Стоя на лыжах, выдавите на каждую единицу площади поверхности снега с силой, меньшей во столько раз, во сколько раз площадь поверхности лыж больше площади подошв обуви.
Наблюдение 2. Легковой автомобиль, в отличие от гусеничного трактора или болотохода, не может проехать по болотистой местности, хотя его вес намного меньше веса трактора. Рассмотрев колёса легкового автомобиля и гусеницы трактора, вы убеждаетесь в том, что площадь поверхности гусениц намного больше, чем колес.
Результат действия силы на поверхность зависит не , только от её значения, но и от площади той поверхности, перпендикулярно к которой она действует.
Убедимся в этом с помощью опытов.
Опыт 1. Заполним стеклянный сосуд песком. На песок поставим столик ножками вверх и на него — гирю массой 2 кг. Результат: столик почти не погрузился в песок (рис. 93, а). Поставим столик ножками на песок и на него — снова гирю массой 2 кг. Результат: ножки стола увязли в песке (рис. 93, б). Возьмём столик с острыми ножками. Поставим его ножками на песок, положив сверху ту же гирю массой 2 кг. Результат: заострённые ножки полностью погрузились в песок (рис. 93, в).
Опыт свидетельствует, что чем меньше площадь опоры столика, тем глубже он погружается в песок под действием одинаковой силы.
Опыт 2. Возьмём два столика. Площадь поверхности ножек одного столика вдвое больше, чем второго. Положим на столики груз, причем на столик с большей площадью поверхности ножек положим вдвое больший груз. Результат действия силы будет одинаковый.
В рассмотренных примерах имела значение сила, действующая перпендикулярно к поверхности тела. Такую силу называют силой давления.
Величину, которая определяется отношением значения силы давления к площади поверхности, на которую она действует, называют давлением.
Давление обозначают малой латинской буквой р. Итак, чтобы определить давление р, нужно силу F , действующую перпендикулярно к поверхности, поделить на площадь этой поверхности S, т. е.
Единицей давления является один паскаль (1 Па), она названа в честь французского учёного Блеза Паскаля. Давление 1 Па создаёт сила давления 1 Н, действующая на поверхность площадью 1 м2, то есть 1 Па = 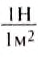
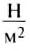
На практике ещё используют кратные единицы давления: гектопаскаль (гПа), килопаскаль (кПа):
Зная давление, можно определить силу давления, действующую на поверхность тела. Давление показывает, какая сила давления действует на единицу площади, поэтому эта сила давления равна произведению давления и площади поверхности: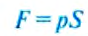
Всем хорошо известно, что во время шитья иглой швеи пользуются напёрстком. Иглу делают очень острой, чтобы умеренной силой пальцев создавать большое давление на ткань и прокалывать её. Но во время нажима пальца на иглу она с такой же силой давит на палец. Конец иглы со стороны ушка делают притуплённым, но во время работы давление на кожу пальца может быть очень большим, достаточным, чтобы ее поранить. Прочный металлический наперсток надежно защищает палец.
Почему подушка мягкая? Почему удобно лежать на перине или на надувном матрасе, а лежать на досках или твёрдой поверхности неудобно ? Оказывается, ощущение мягкости или твёрдости зависит не от свойства материала, а от значения давления на поверхность тела. Сделаем небольшие расчеты.
Будем считать, что масса взрослого человека составляет 60 кг, что равно весу приблизительно 600 Н, а поверхность тела — приблизительно 2 м2. Если человек лежит в кровати на перине, которая прогибается и будто охватывает тело, с ней соприкасается приблизительно четверть всей поверхности его тела, т. е. 0,5 м2 Расчёты по таким данным дают давление 1200 Па. А если человек ляжет на твердую поверхность, то площадь соприкосновения будет составлять около 0,01 м2. Это соответствует давлению 60 000 Па, т. е. давление тела на твёрдую поверхность увеличится в 50 раз, отсюда и неудобства.
В разных областях современной техники приходится решать задачи получения высоких давлений, снижения давления или сохранения его в заданных границах. Проблема давления играет важную роль в транспорте. Дороги и железнодорожные пути должны надежно выдерживать давление разных транспортных средств. Этого достигают, уменьшая вес транспортных средств и увеличивая их площадь опоры. Колеса легкового автомобиля производят на дорогую давление около 300 кПа. Чтобы уменьшить давление на дорогу грузовых автомобилей, их делают многоосными, с колёсами большого диаметра, используют гусеницы. Так, давление, производимое трактором Т-130, вес которого — сотни тысяч ньютонов, равен 27 кПа. Это в 1,5 раза больше давления, которое оказывает на дорогу человек весом 600 Н.
С помощью чрезвычайно тонкого инструмента — жала — оса создаёт давление, соизмеримое с давлением во время взрыва (33 000 000 000 Па).
Кстати:
В Арктике и Антарктике на научных станциях пользуются такими транспортными средствами, как снегоходы «Пингвин» и «Харьковчанка». Снегоход «Харьковчанка» имеет дизельный двигатель мощностью 736 кВт и запас горючего на 1500 км. При массе 35 т он имеет гусеницы шириной 1 м, что даёт ему возможность преодолевать снежную целину, ледовые торосы, крутые склоны. Снегоход имеет утеплённую кабину площадью 25 м2 с мощной отопительной системой, специальной герметичной обшивкой, позволяющей работать даже при морозах ниже — 70 0С. В кабине есть спальные места, радиорубка, рабочая комната, кухня, сушилка, гардероб, санузел. Размеры снегохода: длина — 8,5 м, ширина — 3,5 м, высота — 4,2 м.
Пример №1
С какой целью под головку болта и гайку подкладывают широкие металлические кольца — шайбы, особенно когда скрепляют деревянные детали (рис. 94)?
Ответ: во избежание повреждений деталей уменьшают на них давление за счёт увеличения площади контактной поверхности.
Пример №2
Взрослый человек, у которого площадь подошв обуви равна 450 см2, давит на пол с силой 700 Н. Определите давление человека на пол.
Дано:
F = 700 Н
S = 450 см2 = 0,0450 м2
р — ?
Решение:
Определим давление человека на пол по формуле:
Ответ: давление человека на пол равно 15 556 Па.
Давление жидкостей и газов и закон Паскаля
Опыт 1. Возьмём три цилиндрических сосуда: в один положим деревянный брусок, в другой насыпем какой-либо крупы или песку, а в третий нальём воды (рис. 96).
Деревянный брусок вследствие действия на него силы тяжести будет давить лишь на дно сосуда. Горох будет давить не только на дно, а и на стенки сосуда во всех точках касания горошин. Каждая горошина внутри сжата со всех сторон соседними горошинами и вследствие действия сил упругости сама будет давить во все стороны на горошины. Эти силы давления будут тем больше, чем глубже лежит горошина, т. е. чем больший слой гороха давит на неё сверху.
Вода, налитая в сосуд, вследствие большой подвижности молекул будет давить на дно и стенки сосуда. Каждая частица внутри воды будет сжата со всех сторон соседними частицами и вследствие упругости будет с такой же силой давить на соседние частицы. Эти силы будут тем больше, чем глубже будет находиться частица.
На рис. 97, а изображён прибор, который называют шаром Паскаля. Он имеет в разных местах поверхности маленькие отверстия. К нему присоединена трубка-цилиндр, в которую вставлен поршень. Если набрать в шар воды и нажать на поршень, то увидим, что струйки воды сквозь отверстия бьют во все стороны с одинаковой силой. Это объясняется тем, что поршень давит на поверхность жидкости в трубке. Частицы воды передают давление поршня другим частицам, которые лежат глубже. Таким способом давление поршня передаётся на все частицы воды в шаре. Вследствие этого часть воды выталкивается из шара в виде струек, бьющих изо всех отверстий.
Если шар заполнить дымом, то из всех отверстий шара начнут выходить струи дыма (рис. 97, б).
Это подтверждает, что и газы передают давление, оказываемое на них, во все стороны одинаково.
Давление, оказываемое на жидкость или газ внешними силами, передаётся жидкостью или газом одинаково во всех направлениях.
Это утверждение называют законом Паскаля.
На законе Паскаля основывается действие шприца: давление пальца врача на поршень шприца передаётся без изменений жидкости, содержащейся в нём, и лекарство выходят через иглу шприца.
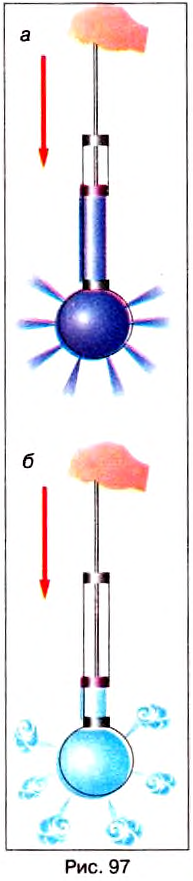
Опыт 2. В стеклянную трубку, нижнее отверстие которой закрыто тонкой резиновой плёнкой, нальём воду (рис. 98, а). Дно трубки прогнётся. Значит, на дно действует сила давления воды. Чем больше наливаем воды, тем более прогибается плёнка. Но каждый раз после того, как резиновое дно прогнулось, вода в трубке находится в равновесии, так как кроме силы тяжести на воду действует сила упругости резиновой плёнки.
Опустим трубку с резиновым дном, в которую налита вода, в более широкий сосуд с водой. Видим, что по мере опускания трубки вниз резиновая плёнка постепенно распрямляется (рис. 98, б). Полное распрямление плёнки показывает, что давление на неё сверху и снизу одинаковое. Значит, в жидкости существует давление, направленное снизу вверх, и на этой глубине оно равно давлению, направленному сверху вниз.
Если выполнить опыт с трубкой, в которой резиновая плёнка закрывает боковое отверстие (рис. 99, а, б), то мы убедимся, что боковое давление жидкости на резиновую плёнку также будет одинаковым с обеих сторон.
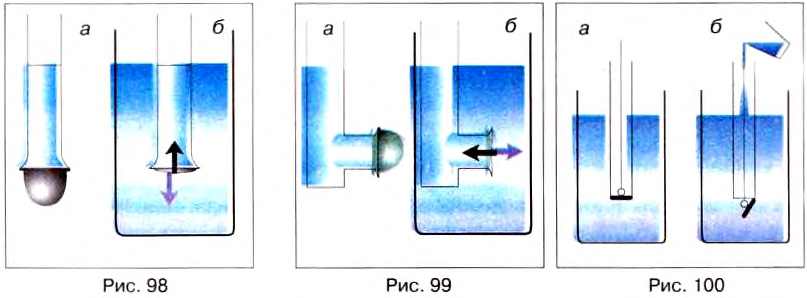
Опыт 3. Сосуд, дно которого может отпадать, опускаем в банку с водой (рис. 100, а). Дно при этом плотно прижимается к краям сосуда давлением воды снизу вверх. Потом в сосуд осторожно нальём воды. Когда уровень воды в ней совпадёт с уровнем воды в банке, дно оторвётся от сосуда (рис. 100, б). В момент отрывания на дно давит сверху столб жидкости в сосуде, а снизу — столб воды, находящейся в банке. Эти давления одинаковы по значениям, однако дно отрывается от сосуда под действием силы тяжести.
Согласно закону Паскаля давление внутри жидкости на одном уровне одинаково во всех направлениях. Давление увеличивается с глубиной.
Давление жидкостей, обусловленное силой тяжести, называют гидростатическим.
А как рассчитать давление жидкости на дно и стенки сосуда ?
Чтобы ответить на этот вопрос припомним, что для того, чтобы определить плотность вещества р, нужно массу тела m разделить на его объём V, т. е.:
Единицей плотности в СИ является один килограмм на кубический метр 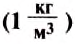
Из формулы для плотности можно определить массу тела. Для этого нужно плотность вещества р умножить на объем тела V, т. е.:
Теперь возвратимся к рис. 98 в опыте 2. Рассчитаем давление, которое создаёт столбик жидкости высотой h на дно цилиндрического сосуда. Мы уже знаем, что давление р равно отношению силы давления F к площади поверхности S, на которую она действует:
В нашей задаче сила давления равно весу жидкости Р :
где m — масса жидкости, которую можем определить через плотность жидкости 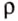
Объём цилиндрического столба жидкости V равен произведению площади дна сосуда S и высоты уровня жидкости над дном h: 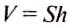
С учётом этих соотношений формула для давления приобретёт окончательный вид:
Видим, что гидростатическое давление на любой глубине внутри жидкости зависит только от ее плотности 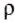
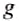
Гидростатическое давление жидкости не зависит ни от формы сосуда, ни от массы жидкости в сосуде, ни от площади его дна. Согласно закону Паскаля это давление на одном уровне жидкости одинаково действует и на дно, и на стенки сосуда.
Кстати:
В 1648 г. Блез Паскаль провёл интересный опыт. Он вставил в закрытую деревянную бочку, наполненную водой, тонкую трубку и, поднявшись на балкон второго этажа, влил в эту трубку кварту
(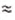
Пример №3
Чем объяснить, что вёдра в форме срезанного конуса очень распространены (рис. 101), хотя они менее устойчивы, и из них больше расплёскивается вода по сравнению с ведрами цилиндрической формы и такой же высоты? Кроме того, конусообразные ведра неудобно нести, так как приходится широко расставлять руки.
Ответ: оказывается, в большинстве случаев вёдра выходят из строя из-за того, что у них выпадает дно. Следовательно, прочность дна определяет долговечность ведра. В ведре конической формы площадь дна меньше, чем в ведре цилиндрической формы такой же вместимости, а потому сила давления на дно меньше. Это единственное преимущество конических ведер оправдывает все другие их недостатки.
Пример №4
Наибольшая глубина, на которой учёные с корабля «Витязь» выловили рыбу, составляет 7200 м. Какое давление создаёт вода на этой глубине?
Дано:
h = 7200м
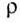
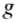
p = ?
Решение:
Давление создаваемое морской водой на глубине, определим по формуле: 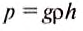
Подставив значения величин, получим:
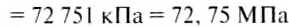
Ответ: 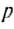
Давление и закон Архимеда
Почему жители севера для передвижения по снегу используют лыжи? Почему женщина, обутая летом в обувь на шпильках, оставляет на мягком асфальте заметные и глубокие следы? Зачем лезвия ножей время от времени натачивают? для чего у гвоздя есть острие? Попытаемся выяснить ответы на эти вопросы.
Давление твердых тел на поверхность и сила давления
Наблюдаем последствия действия силы: Одно из последствий действия силы — деформация тел, при этом чем большая сила действует на тело, тем больше будет деформация. Деформация зависит и от других факторов, в частности от площади поверхности, по которой распределяется действие силы.
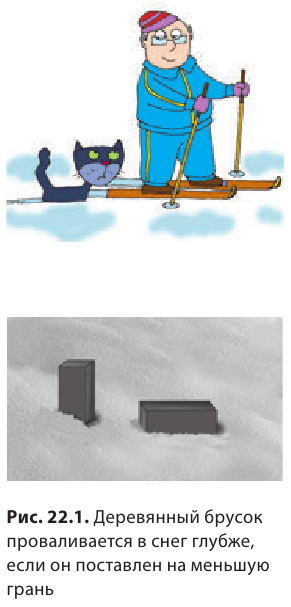
В большинстве случаев чем больше площадь поверхности, на которую действует данная сила, тем меньше будет деформация. Проиллюстрируем это утверждение с помощью простого опыта: поставим деревянный брусок на снег сначала гранью меньшей площади, а затем — гранью большей площади (рис. 22.1).
В первом случае снег деформируется сильнее (брусок глубже провалится в снег), хотя в обоих случаях сила, действующая на снег со стороны бруска (то есть вес бруска), одинакова. Можно провести еще один опыт: нажмите с одинаковой небольшой силой на поверхность песка сначала раскрытой ладонью, а затем пальцем — и вы увидите, в каком случае глубина следа будет больше (рис. 22.2).
Определение давления
Для характеристики зависимости результата действия силы от площади поверхности, на которую действует эта сила, используют такое понятие, как давление.
Давление — это физическая величина, которая характеризует результат действия силы и равна отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности: 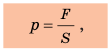
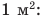
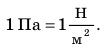
Как можно увеличить или уменьшить давление
Из определения давления 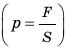
Пример №5
Сравните давления, которые оказывают на поверхность снега юные спортсмены — турист и лыжник. Масса каждого из них вместе со снаряжением равна 63 кг. Площадь подошвы ботинка туриста — приблизительно 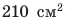
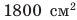
Дано:
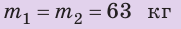
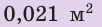
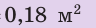
Найти:

Решение:
По определению давления:
Здесь 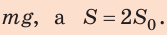
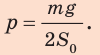
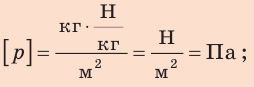
для лыжника:
Анализ результатов. Давление, создаваемое туристом, приблизительно в 8,6 раза больше давления, создаваемого лыжником. Это реальный результат, ведь при равных силах большее давление создает та сила, которая действует на меньшую площадь.
Ответ:
Итоги:
Давление p — это физическая величина, которая характеризует результат действия силы и равна отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности: 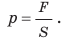
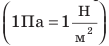
Давление газов и жидкостей. Закон паскаля
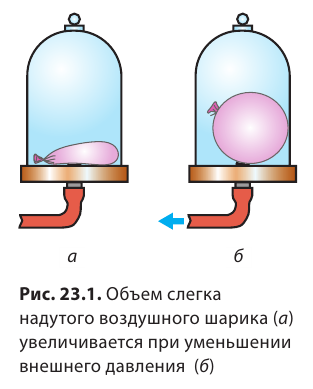
Почему при надувании резинового воздушного шарика увеличивается его объем? ответ понятен: в шарике становится больше воздуха. а можно ли увеличить объем шарика без того, чтобы его надувать? Почему налитая в сосуд жидкость создает давление не только на дно сосуда, но и на его боковые поверхности? Почему водитель, нажимая на тормоз, может остановить тяжелый автомобиль? Попробуем «разгадать» эти загадки.
Почему газы создают давление
Положим слегка надутый завязанный воздушный шарик под колокол воздушного насоса (рис. 23.1, а). Если из под колокола откачивать воздух, объем шарика будет увеличиваться (рис. 23.1, б). Почему это происходит?
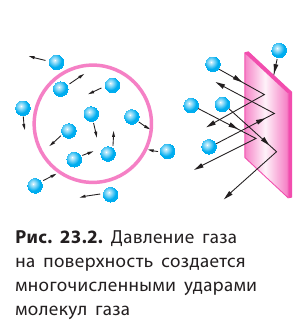
И снаружи шарика, и внутри него находится воздух (газ). Газ состоит из частиц (атомов и молекул), которые непрерывно движутся во всех направлениях и «бомбардируют» резиновую пленку, создавая на нее давление (рис. 23.2). Понятно, что сила удара одной частицы очень мала. Однако частиц в газе очень много — всего за 1 секунду количество их ударов по поверхности пленки таково, что для его записи требуется число с 23 нулями!
Поэтому общая сила, с которой ударяет такое огромное количество частиц, является значительной. Воздух внутри и снаружи шарика оказывает давление соответственно на внутреннюю и внешнюю поверхности резиновой пленки.
Если эти давления одинаковы, резиновая пленка не растягивается. А вот если давление внутри шарика становится больше внешнего давления, то шарик увеличивает свой объем. Надеемся, теперь вы сможете объяснить, почему воздушный шарик раздувается и тогда, когда мы его надуваем, и тогда, когда откачиваем воздух снаружи шарика.
- Заказать решение задач по физике
От чего зависит давление газов
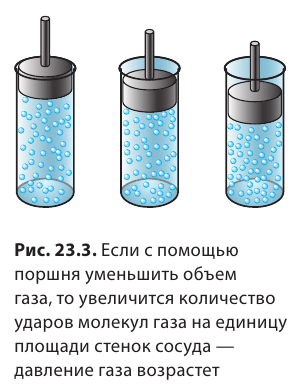
Давление газа создается ударами его частиц, поэтому увеличение как количества ударов, так и силы ударов приводит к увеличению давления газа. Следовательно, давление газов можно увеличить двумя способами. Первый способ — увеличить плотность газа 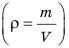
Второй способ — увеличить температуру газа. Чем выше температура газа, тем быстрее движутся его частицы. Удары частиц о стенки сосуда становятся чаще, сила их ударов возрастает, и в результате давление газа в сосуде увеличивается. Соответственно уменьшение давления газа будет происходить при уменьшении плотности или температуры газа.
Исследование давления жидкостей
В отличие от твердых тел жидкости легко изменяют свою форму — они приобретают форму того сосуда, в котором находятся, другими словами, жидкости текучи. Именно поэтому жидкости оказывают давление и на дно, и на боковые стенки сосуда, в котором находятся (в отличие от твердых тел, которые оказывают давление только на ту часть поверхности, на которую опираются). Если в боковой стенке сосуда, заполненного жидкостью, сделать отверстия, то жидкость польется через них (рис. 23.4).
Следствием текучести жидкостей является также то, что на любое погруженное в жидкость тело жидкость давит со всех сторон.
Закон Паскаля
Благодаря своей текучести жидкость способна передавать давление по всему объему сосуда, в котором находится. Сделав иглой небольшие отверстия в полиэтиленовом пакете, наберем в пакет воду и завяжем. Нажмем на пакет — вода будет выливаться из всех отверстий (рис. 23.5).
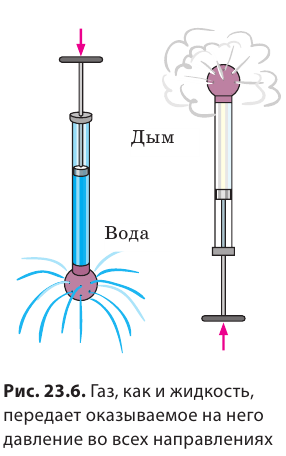
Аналогичный эксперимент можно провести с воздухом или другим газом (рис. 23.6). Опираясь на подобные опыты, французский физик Б. Паскаль открыл закон, который сейчас называется закон Паскаля: давление, оказываемое на неподвижную жидкость, передается жидкостью одинаково во всех направлениях. То же самое можно сказать о газах.
Применяем закон Паскаля:
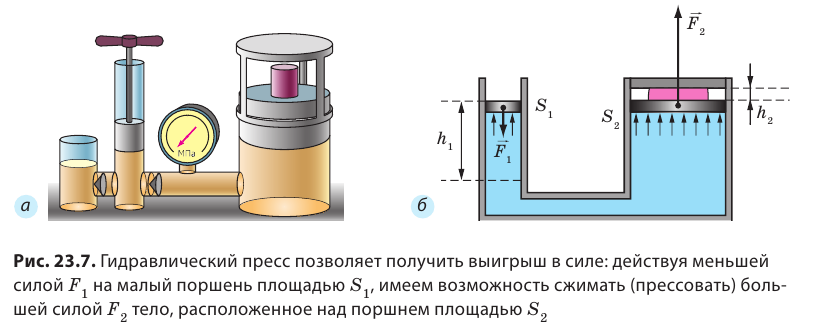
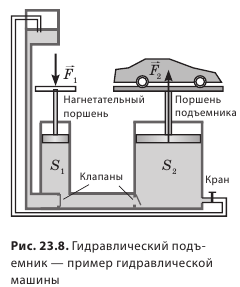
Свойство жидкостей и газов передавать давление во всех направлениях мы наблюдаем в повседневной жизни; это свойство широко используют в технике. Благодаря ему мы имеем возможность слышать, ведь воздух передает звук; работает наша сердечнососудистая система, ведь несмотря на то, что кровеносные сосуды имеют большое количество изгибов, давление, создаваемое сердцем, передается во все части тела. На законе Паскаля основана система торможения многих транспортных средств, действие домкратов, насосов и других гидравлических машин. Рассмотрим принцип действия гидравлических машин на примере гидравлического пресса, который применяют для прессования фанеры и картона, отжима растительных масел, изготовления деталей машин и механизмов и т. п.
Гидравлический пресс — это простейшая гидравлическая машина, которую используют для создания больших сил давления. Гидравлический пресс состоит из двух соединенных между собой цилиндров разного диаметра, заполненных рабочей жидкостью (чаще машинным маслом) и закрытых подвижными поршнями (см. рис. 23.7). Если к поршню меньшего цилиндра приложить силу 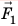
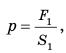
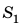
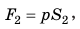
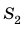
Поскольку 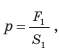
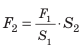
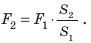
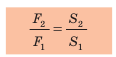
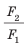
Итоги:
Газ оказывает давление на поверхность в результате многочисленных ударов об эту поверхность частиц газа. Давление газа возрастает при увеличении плотности или температуры газа и уменьшается при уменьшении плотности или температуры газа. Вследствие своей текучести жидкость оказывает давление на дно и боковые стенки сосуда, а также на любое тело, погруженное в данную жидкость. Давление, оказываемое на неподвижную жидкость, передается этой жидкостью одинаково во всех направлениях (закон Паскаля). Свойство жидкостей передавать давление одинаково во всех направлениях положено в основу действия гидравлических машин. Сила, действующая со стороны жидкости на большой поршень гидравлической машины, больше силы, действующей на малый поршень, во столько раз, во сколько раз площадь большого поршня больше площади малого:
Гидростатическое давление
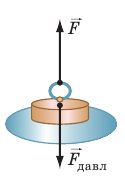
На рис. 24.1 изображен современник Блеза Паскаля, стоящий на кожаной подушке, заполненной водой. с подушкой соединена открытая сверху трубка — ее исследователь держит в руках. Почему доска, на которой стоит человек, не сжимает подушку полностью и не вытесняет через трубку всю воду наружу?
Получаем формулу для расчета:
Гидростатического давления Вы уже знаете, что в результате притяжения к Земле и благодаря собственной текучести жидкость оказывает давление как на дно, так и на стенки сосуда, в котором содержится. Жидкость оказывает давление и на любое погруженное в нее тело. Давление неподвижной жидкости называют гидростатическим давлением.
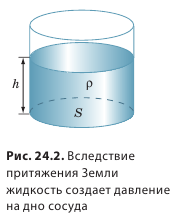
Определим гидростатическое давление на дно сосуда. Чтобы упростить расчеты, возьмем цилиндрический сосуд с площадью дна S. Пусть в сосуд налита жидкость плотностью ρ, а высота столба жидкости в сосуде — h (рис. 24.2).
Чтобы вычислить давление, которое создает жидкость на дно сосуда, следует силу F, действующую на дно, разделить на площадь S дна: 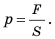
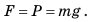
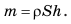

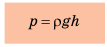
Проводим исследования и делаем выводы:
Зависимость гидростатического давления от высоты столба жидкости впервые продемонстрировал Блез Паскаль. Взяв бочку, до краев заполненную водой, исследователь герметично закрыл ее крышкой со вставленной длинной тонкой трубкой. Поднявшись на балкон второго этажа жилого дома, Паскаль вылил в трубку всего один стакан воды. Вода заполнила всю трубку и создала на стенки и дно бочки такое огромное давление, что в боковых стенках бочки появились щели (рис. 24.3).
Обратите внимание! Согласно закону Паскаля давление жидкости передается во всех направлениях, а значит, по формуле 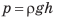
Пример №6
На дне бассейна расположено круглое отверстие, закрытое пробкой радиусом 5 см. Какую силу нужно приложить к пробке, чтобы вынуть ее из отверстия, если высота воды в бассейне 2 м? Массой пробки и силой трения между пробкой и отверстием пренебречь. Анализ физической проблемы. Вынуть пробку мешает сила давления воды в бассейне. Массу пробки и силу трения учитывать не нужно, поэтому сила, необходимая для того, чтобы вынуть пробку из отверстия, по значению должна быть не меньше, чем сила гидростатического давления воды на пробку: 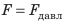
Уровнем называют любую горизонтальную поверхность.
Дано:
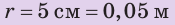
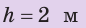
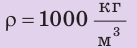
найти:
Решение:
По определению давления:
Здесь 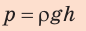
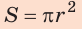
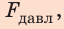
Так как 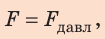
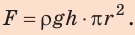
Ответ: следует приложить силу не менее чем 157 Н.
Итоги:
В результате притяжения к Земле жидкости создают давление на дно и стенки сосудов, а также на любое погруженное в них тело. Давление p неподвижной жидкости называют гидростатическим давлением — оно зависит только от плотности ρ жидкости и высоты h столба жидкости. Гидростатическое давление вычисляют по формуле 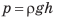
Атмосферное давление и его измерение. Барометры
Когда мы делаем глоток чая, то вряд ли размышляем над физикой этого процесса. При этом глотание, как и многие другие процессы, происходит благодаря давлению воздуха вокруг нас — атмосферному давлению. откроем для себя некоторые важные свойства атмосферного давления и научимся его измерять.
Что такое атмосфера
Вы хорошо знаете, что наша планета Земля окружена воздушной оболочкой, которую называют атмосферой (в переводе с греческого — «пар» и «сфера») (рис. 25.1). Почему же существует воздушная оболочка Земли? Воздух состоит из молекул и атомов. Молекулы и атомы имеют массу, поэтому они притягиваются к Земле благодаря действию силы тяжести. Все огромное количество молекул газов, составляющих атмосферу, находится в непрерывном хаотическом движении — они все время сталкиваются, отскакивают друг от друга, изменяют значение и направление скорости своего движения… Именно поэтому они не «падают» на Землю, а находятся в пространстве вблизи нее.
По подсчетам, атмосфера Земли имеет массу около 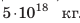
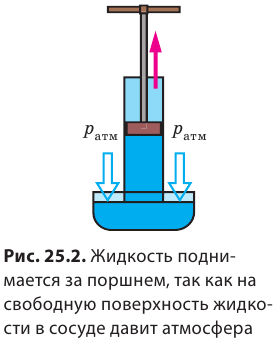
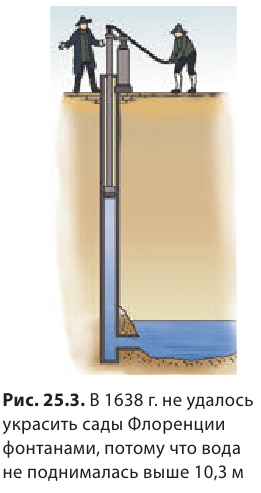
Кстати, долгое время поднятие жидкости за поршнем, движущимся вверх, приводилось как одно из доказательств известного принципа Аристотеля «Природа боится пустоты». Однако в середине XVII в. при строительстве фонтанов во Флоренции столкнулись с непонятным явлением: оказалось, что вода, которая всасывается насосами, не поднимается выше 10,3 м (рис. 25.3). Галилео Галилей предложил разобраться в этом своим ученикам — Эванджелисте Торричелли (1608–1647) и Винченцо Вивиани (1622–1703). Разбираясь с данной проблемой, Э. Торричелли впервые доказал существование атмосферного давления.
Измерение атмосферное давления
Для удобства проведения опытов Э. Торричелли догадался заменить воду жидкостью с намного большей плотностью. Стеклянную трубку длиной около метра, запаянную с одного конца, ученый доверху наполнил ртутью. Затем, плотно закрыв отверстие, он перевернул трубку, опустил ее в чашу с ртутью и открыл отверстие — часть жидкости из трубки вылилась в чашу. В трубке остался столб ртути высотой приблизительно 760 мм, а над ртутью образовалась пустота (рис. 25.4). Проведя множество опытов, Торричелли установил: высота столба ртути, остающейся в трубке (760 мм), не зависит ни от длины трубки, ни от ее диаметра, — эта высота немного изменяется только в зависимости от погоды.
Торричелли сумел также объяснить, почему высота столба ртути имеет именно такую высоту. Однородная жидкость в трубке и чаше неподвижна. Значит, согласно закону Паскаля давление на поверхность ртути со стороны атмосферы и гидростатическое давление столба ртути в трубке одинаковы. То есть давление столба ртути высотой 760 мм равно атмосферному давлению.давление, которое создает столб ртути высотой 760 мм, называют нормальным атмосферным давлением: 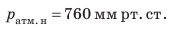
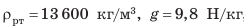
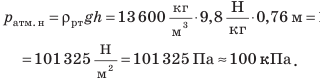
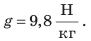
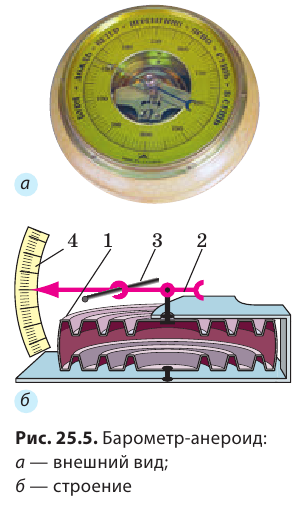
Конструкция барометра-анероида
Если к трубке Торричелли присоединить вертикальную шкалу (линейку), то получим простейший барометр — прибор для измерения атмосферного давления. Действие такого барометра основано на том, что столб жидкости прекращает подниматься (опускаться) как только гидростатическое давление столба жидкости становится равным атмосферному давлению. Барометр Торричелли — достаточно точный прибор, однако большой размер, ядовитые пары ртути и стеклянная трубка делают его неудобным для повседневного использования. Сейчас широко применяют барометры анероиды — приборы для измерения атмосферного давления, работающие без помощи жидкости (рис. 25.5). Главная часть барометраанероида — легкая и упругая пустая металлическая коробочка 1 с гофрированной (ребристой) поверхностью. Воздух в коробочке находится при сниженном давлении. К стенке коробочки прикреплена стрелка 2, насаженная на ось 3. Конец стрелки передвигается по шкале 4, размеченной в миллиметрах ртутного столба или паскалях. Все детали барометра размещены в корпусе, передняя часть которого закрыта стеклом. Изменение атмосферного давления вызывает изменение силы, сжимающей стенки коробочки. Соответственно изменяется изгиб стенок коробочки. Изгиб стенок передается стрелке и вызывает ее движение.
Барометры анероиды более удобны в использовании, чем ртутные приборы: они легкие, компактные и безопасные.
Определение зависимости атмосферного давления от погоды и высоты
Наблюдая за барометром, можно легко прогнозировать изменение погоды. Например, перед ненастьем атмосферное давление обычно падает. Показания барометра зависят не только от погоды, а и от высоты над уровнем моря. Чем выше место наблюдения над уровнем моря, тем меньше атмосферное давление. Вблизи поверхности Земли через каждые 11 м высоты атмосферное давление уменьшается приблизительно на 1 мм рт. ст. Поскольку атмосферное давление зависит от высоты, барометр можно проградуировать таким образом, чтобы по давлению воздуха определять высоту. Так был изобретен альтиметр — прибор для измерения высоты (рис. 25.6).
Итоги:
Воздух имеет массу. Из-за притяжения Земли верхние слои атмосферы (воздушной оболочки Земли) давят на нижние. Давление воздуха на поверхность Земли и на все тела вблизи нее называют атмосферным давлением. Точное измерение атмосферного давления обеспечивает ртутный барометр (барометр Торричелли). Давление столба ртути высотой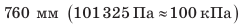
- Механическое давление в физике
- Столкновения в физике
- Рычаг в физике
- Блоки в физике
- Вес тела в физике
- Закон всемирного тяготения
- Свободное падение тела
- Равнодействующая сила и движение тела под действием нескольких сил
Почему нам довольно трудно идти по рыхлому снегу так, чтобы не провалиться, однако на лыжах можно спокойно катиться по его поверхности?
На данном уроке мы ответим на этот вопрос и на многие другие, познакомимся с новой величиной в физике и рассмотрим ее свойства.
Что такое давление?
Так почему человек, идущий на лыжах, не проваливается в снег?
Этого не происходит по одной простой причине: площадь поверхности лыжи примерно в двадцать раз больше, чем у обычной подошвы (рисунок 1).
Так и искусный йог может спокойно сидеть на гвоздях (рисунок 2). Ведь в сидячем положении площадь соприкосновения тела с ковриком из гвоздей больше, чем у двух ступней.
Оказывается, результат действия силы зависит не только от величины этой силы, но и от площади той поверхности, перпендикулярно которой она действует. Поэтому в физике ввели новую величину, которую назвали давлением.
Давление — это величина, равная отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности:
$p = frac{F}{S}$,
где $F$ — сила, действующая на поверхность, $S$ — площадь этой поверхности, а $p$ — искомое давление.
Рассмотрим давление на еще одном примере. Если мы положим деревянный брусок на доску, лежащую на двух опорах (рисунок 3), горизонтально, то доска не прогнется. А если мы поставим его вертикально? Тогда уменьшится площадь соприкосновения. Значит, увеличится и давление. Доска прогнется.
Единицы измерения давления
Какие вы знаете единицы давления?
Мы уже знаем, что единица измерения силы — ньютон, а единица измерения площади — $м^2$. Тогда из формулы $p = frac{F}{S}$ получается, что единица измерения давления — $frac{Н}{м^2}$.
В честь французского ученого Блеза Паскаля (рисунок 4) ее и назвали паскалем:
$1 space Па = 1 frac{Н}{м^2}$.

Также часто используются и другие единицы давления: гектопаскаль ($гПа$) и килопаскаль ($кПа$).
$1 space кПа = 1000 space Па$,
$1 space Па = 0.001 space кПа$.
$1 space гПа = 100 space Па$,
$1 space Па = 0.01 space гПа$.
Пример задачи
Найдите давление, c которым ваза с цветами давит на стол, если площадь ее дна — $100 space см^2$ , а масса — $2 space кг$. Ускорение свободного падения принять за $10 frac{Н}{кг}$ .
Дано:
$S = 100 space см^2$
$m = 2 space кг$
$g = 10 frac{Н}{кг}$
СИ:
$S = 0.01 space м^2$
$p — ?$
Показать решение и ответ
Скрыть
Решение:
Давление рассчитывается по формуле:
$p = frac{F}{S}$.
На вазу с цветами действует сила тяжести:
$F = F_{тяж} = mg$.
Подставим это значение в формулу для давления и рассчитаем его:
$p = frac{mg}{S}$,
$p = frac{2 space кг cdot 10 space frac{Н}{кг}}{0.01 space м^2} = frac{20 space Н}{0.01 space м^2} = 2000 space Па = 2 space кПа$.
Ответ: $p = 2 space кПа$.
Как можно изменить давление?
Не всегда людям удобно большое давление. Как же быть, если сила, с которой массивный объект действует на какую-либо поверхность, оказывается слишком велика?
Мы всегда можем изменить площадь соприкосновения этого объекта с поверхностью, тем самым изменив и само давление.
Например, шины грузовых машин делают несколько шире, чем у легковых (рисунок 5). Так, площадь соприкосновения грузовой машины с дорогой будет больше, а давление станет меньше.
Лезвия ножниц и ножей делают острее (рисунок 6), тем самым уменьшая площадь соприкосновения и увеличивая давление. Поэтому даже при прикладывании маленькой силы мы с легкостью можем разрезать даже твердые и большие предметы.
На каком опыте можно показать, что действие силы зависит от площади опоры?
Например, можно взять пластилин, глину или другое достаточно легко деформирующееся тело и надавить на него сначала одним пальцем, а потом целым кулаком.
Регулируя свою силу так, чтобы в двух случаях она была примерно одинаковой, вы сможете увидеть, что в первом случае пластилин деформируется гораздо сильнее (ямка получилась гораздо глубже), чем во втором.
То же самое можно проделать и с вашей ладошкой: надавить на нее большим пальцем будет больнее, чем целым кулаком, хотя кажется, что все должно быть с точностью до наоборот.
Упражнения
Упражнение №1
Выразите в паскалях давление: $5 space гПа$; $0.02 frac{Н}{м^2}$; $0.4 space кПа$; $10 frac{Н}{м^2}$.
Выразите в гектопаскалях и килопаскалях давление: $10 space 000 space Па$; $5800 space Па$.
Показать ответ
Скрыть
Выразим давление в паскалях:
$p_1 = 5 space гПа = 500 space Па$,
$p_2 = 0.02 frac{Н}{см^2} = 0.02 cdot 10^4 space Па = 200 space Па$,
$p_3 = 0.4 space кПа = 400 space Па$,
$p_4 = 10 frac{Н}{м^2} = 10 cdot 10^4 space Па = 100 space 000 space Па$.
Выразим давление в гектопаскалях и килопаскалях:
$p_5 = 10 space 000 space Па = 100 space гПа = 10 space кПа$,
$p_6 = 5800 space Па = 58 space гПа = 5.8 space кПа$.
Упражнение №2
Рассчитайте давление, производимое на пол мальчиком, масса которого $45 space кг$, а площадь подошв его ботинок, соприкасающихся с полом, равна $300 space см^2$.
Дано:
$S = 300 space см^2$
$m = 45 space кг$
$g = 10 frac{Н}{кг}$
СИ:
$S = 0.03 space м^2$
$p — ?$
Показать решение и ответ
Скрыть
Решение:
Давление рассчитывается по формуле:
$p = frac{F}{S}$.
Какая сила действует на неподвижно стоящего мальчика? На него действует сила тяжести. Также мальчик с каким-то весом действует на пол. В данном случае эти силы равны: $F = F_{тяж} = P = gm$.
Подставим в формулу для давления и рассчитаем его:
$p = frac{F}{S} = frac{P}{S} = frac{gm}{S}$,
$p = frac{10 frac{Н}{кг} cdot 45 space кг}{0.03 space м^2} = frac{450 space Н}{0.03 space м^2} = 15 space 000 space Па = 15 space кПа$.
Ответ: $p = 15 space кПа$.
Упражнение №3
Гусеничный трактор ДТ-75М массой $6610 space кг$ имеет опорную площадь обеих гусениц $1.4 space м^2$. Определите давление этого трактора на почву. Во сколько раз оно больше давления, производимого мальчиком из предыдущего упражнения?
Дано:
$m = 6610 space кг$
$S = 1.4 space м^2$
$g = 10 frac{Н}{кг}$
$p_м = 15 space кПа$
$p — ?$
$frac{p}{p_м} — ?$
Показать решение и ответ
Скрыть
Решение:
Рассчитаем давление, которое оказывает трактор на землю:
$p = frac{F}{S} = frac{gm}{S}$,
$p = frac{10 frac{Н}{кг} cdot 6610 space кг}{1.4 space м^2} = frac{66 space 100 space Н}{1.4 space м^2} approx 47 space 214 space Па approx 47 space кПа$.
Узнаем во сколько раз это давление больше, чем давление, которое оказывает мальчик на землю:
$frac{p}{p_м} = frac{47 space кПа}{15 space кПа} approx 3$.
То есть давление трактора на почву в 3 раза больше давления, производимого мальчиком.
Ответ: $p approx 47 space кПа$, в 3 раза больше.
Упражнение №4
Человек нажимает на лопату с силой $600 space Н$. Какое давление оказывает лопата на почву, если ширина ее лезвия $20 space см$, а толщина режущего края $0.5 space мм$? Зачем лопаты остро затачивают?
Дано:
$F = 600 space Н$
$a = 20 space см$
$b = 0.5 space мм$
СИ:
$a = 0.2 space м$
$b = 0.0005 space м$
$p — ?$
Показать решение и ответ
Скрыть
Решение:
Для того, чтобы рассчитать давление, нам нужно знать силу и площадь. В данном случае нам неизвестна площадь, но известны ширина и толщина интересующей нас поверхности, которая оказывает давление:
$S = a cdot b$,
$S = 0.2 space м cdot 0.0005 space м = 0.0001 space м^2$.
Рассчитаем давление:
$p = frac{F}{S}$,
$p = frac{600 space Н}{0.0001 space м^2} = 6 space 000 space 000 space Па = 6000 space кПа$.
Очевидно, что чем меньше будет площадь лезвия лопаты, тем проще будет копать. При одинаковых усилиях мы будем оказывать большее давление. Соответственно, лопаты остро затачивают для того, чтобы увеличить оказываемое ими давление.
Ответ: $p = 6000 space кПа$.
Упражнение №5
Мальчик массой $45 space кг$ стоит на лыжах. Длина каждой лыжи $1.5 space м$, ширина $10 space см$. Какое давление оказывает мальчик на снег? Сравните его с давлением, которое производит мальчик, стоящий без лыж.
Дано:
$m = 45 space кг$
$a = 1.5 space м$
$b = 10 space см$
$p_м = 15 space кПа$
$g = 10 frac{Н}{кг}$
$p — ?$
$frac{p_м}{p} — ?$
Показать решение и ответ
Скрыть
Решение:
Рассчитаем площадь поверхности одной лыжи:
$S_1 = a cdot b$,
$S_1 = 1.5 space м cdot 0.1 space м = 0.15 space м^2$.
Лыж у нас две. Тогда общая площадь поверхности обоих лыж:
$S = 2S_1$,
$S = 2 cdot 0.15 space м^2 = 0.3 space м^2$.
Теперь мы можем рассчитать давление, которое оказывает на снег мальчик на лыжах:
$p = frac{F}{S} = frac{gm}{S}$,
$p = frac{10 frac{Н}{кг} cdot 45 space кг}{0.3 space м^2} = frac{450 space Н}{0.3 space м^2} = 1500 space Па = 1.5 space кПа$.
Сравним это давление с давлением мальчика без лыж:
$frac{p_м}{p} = frac{15 space кПа}{1.5 space кПа} = 10$.
Получается, что использование лыж позволяет мальчику уменьшить давление в 10 раз.
Ответ: $p = 1.5 space кПа$, в 10 раз меньше.
Задание
В стеклянную емкость насыпьте песка. Наполните пластиковую бутылку с длинным горлышком водой, закройте крышкой и поставьте на песок. Затем переверните бутылку вверх дном и снова поставьте на песок. Объясните, почему во втором случае бутылка глубже вошла в песок.
Когда мы перевернули бутылку, мы уменьшили площадь ее поверхности, которая оказывает давление на песок ($p = frac{F}{S}$). Вес бутылки при этом не изменился ($F = P = gm$). Таким образом мы увеличили давление — бутылка глубже ушла в песок.
План урока:
Можно ли бежать по снегу?
Способы изменения давления
Давление газа
Закон Паскаля
Давление жидкости
Сообщающиеся сосуды
Можно ли бежать по снегу?
В соревнованиях, когда одна команда бежит на лыжах по рыхлому снегу, а другая без лыж победит, конечно же, команда с лыжами. Все дело в лыжах. Когда человек стоит на лыжах, его вес равномерно распределяется по всей площади лыж. Нетрудно сравнить площадь двух лыж и площадь подошв обуви.
Площадь лыж больше площади подошв. Если одинаковый вес человека распределить на разные площади, получится, что каждой единице площади лыж достанется веса меньше, чем такой же единице площади подошв. (Чтобы лучше понять это, надо представить простую ситуацию: на разные по размерам куски хлеба намазать по одинаковому количеству сливочного масла. На маленьком куске хлеба получится толстый слой масла, а на большом — масло размажется очень тонко).
Сила, которая давит на длинные лыжи и небольшие подошвы – это вес человека. А вот сила, которая приходится на единицу площади лыжи или подошвы – это уже не полный вес человека, а лишь маленькая часть этого веса. Эту силу в физике называют давлением.
Значит, команда на лыжах выиграла, так как оказывала на снег меньшее давление, и передвигаться ей, не проваливаясь, было легче.
Нужно отличать давление от силы давления. В примере в роли силы давления выступает вес человека, а давление – это часть веса, которая достается единице площади.
Давление принято обозначать буквой p (маленькая латинская буква) и находить по правилу:
p = F/S.
Достаточно понятная формула: «силу давления F разделить (распределить) на площадь S».
Источник
Давление измеряют и другими единицами:
Источник
Давление оказывают тела не только своим весом. Когда, например, режут хлеб или сыр на части, то нож разрезает продукты под действием мышечной силы руки.
Зная давление, можно найти силу, которая действует на поверхность:
F = p ∙ S
Способы изменения давления
Жарким летним днем, когда асфальт будто плавится, на нем остаются следы.
Какая обувь оставляет самые заметные, глубокие следы? Несомненно, ответ прост: это шпильки женских туфель. Маленькая площадь, следовательно, большое давление – и видимый результат.
Иногда давление необходимо сделать большим, иногда — маленьким.
Большое давление нужно там, где имеют дело с режущими и колющими инструментами. Необходимо, чтобы они были остро заточены, чтобы площадь соприкосновения была минимальной. Если нажать посильнее, то можно получить огромные давления. Резец токарного станка срезает стружку, оказывая давление на деталь 2,45 ∙ 109 Па.
Источник
В рукопашном бое востока преобладают колющие и рубящие удары пальцами рук, ног и ребром ладони. Обладая маленькой массой, можно нанести резкий болевой удар, ведь площадь кончиков пальцев или ребра ладони значительно меньше площади всей ладони или кулака. А значит, при одинаковой силе можно оказать большее давление на место удара.
А какое давление оказывает лезвие из дамасской стали, если легкая шелковая лента, упав на саблю, перерезается пополам!
В тех случаях, когда давление должно быть маленьким, сила должна быть тоже небольшой, а это в современных технологиях встречается редко. Тогда для уменьшения давления нужно увеличить площадь опоры.
Гусеницы тракторов, вездеходов значительно уменьшают давление на почву (всего 40 — 50 кПа), поэтому этот вид транспорта хорошо проходим даже в условиях болота. Для сравнения давление, которое оказывают колеса легкового автомобиля на дорогу равно 200 – 300 кПа, причем вес автомобиля значительно меньше, чем у трактора. Человек для прохождения по болотистой почве применяет специальные болотоходы, а по снегу – снегоходы.
Для того, чтобы дома и другие строения не давали осадку, необходимо под них подводить широкий фундамент (увеличение площади). Известная всему миру Останкинская башня, высотой 533 м, давит своим фундаментом на землю всего в 270 кПа (как легковой автомобиль). Таким же фундаментом для железнодорожных рельсов являются шпалы, уменьшающие давление вагонов на рельсы.
Для похода лучше выбирать рюкзак с широкими лямками, даже не нужно объяснять, почему.
Животным природа подарила возможность учитывать и использовать давление:
- клыки (хищники легко разрывают ими мясо);
- когти (кошки свободно забираются на дерево, спасаясь от собаки);
- острые зубы (пираньи – хищные рыбы пресных вод в считанные секунды обгладывают свои жертвы):
- клювы (дятел быстро долбит кору деревьев, находя там жучков для еды);
- острые носы (комар мгновенно протыкает кожу людей и животных и высасывает кровь);
Приведенные примеры говорят о том, как животные приспособились к борьбе за существование.
Итак, давление учитывает и человек, и природа, стремясь держать его большим или маленьким в нужных случаях.
Давление газа
Воздушные шары и мыльные пузыри знакомы всем взрослым и детям. Это обязательный атрибут игр или праздников. А как получить такой шарик? Он наполняется воздухом, который человек вдувает в шарик при выдохе. С каждым выдохом шарик растет все больше, и делается все более упругим. На резину шарика воздух давит, стараясь растянуть его в разные стороны. Силе давления противостоит сила упругости деформированного шарика, и нужно вовремя остановиться, иначе сила давления перерастет силу упругости, произойдет громкий хлопок – шарик лопнет.
Твердое тело весом давит на часть поверхности, на которой стоит (если ведро стоит на полу, то оно и давит только на пол), а газ действует во всех направлениях одинаково, поэтому мыльные пузыри имеют форму шара. Форму воздушного шара определяет резина, из которой он изготовлен. Если резина везде одинакова, то шар будет круглым. Если резина имеет в разных частях шара разную упругость, то и шар надуется по-разному, и будет иметь заданную форму.
Молекулы газообразного вещества мечутся беспорядочно и хаотично, но такой хаос большого количества частиц обеспечивает некий порядок: в любых направлениях зигзагообразными траекториями движется примерно одинаковое количество молекул. Суммарная сила удара сразу всех молекул, действующая на единицу площади, и образует давление газа.
Источник
Если накачивать насосом камеру велосипеда или мяча, то с каждым качком камера становится будто бы более твердой, потому что молекулы воздуха все прибывают и прибывают, сила суммарного удара по стенкам камеры становится все больше и больше. А значит, давление растет. Если воздух выходит, то камера на глазах «худеет», давление уменьшается. С ростом числа молекул связано увеличение массы газа, а уменьшение числа молекул ведет к уменьшению массы. Поэтому давление газа зависит от его массы, которую опытным путем гораздо легче определить, чем само давление.
С повышением температуры тела молекулы перемещаются быстрее. Чем выше скорость, тем сильнее молекулы ударяются о сосуд, в котором газ находится. Значит, чем температура выше, тем значительнее давление, оказываемое газом.
Еще интересный пример изменения давления. Надо взять бумажный пакет, надуть его и резко ударить по нему ладонью. Хлопок, и пакет разорван. Все очень быстро и просто, а ведь здесь произошли вполне объяснимые физические процессы. Кулек под ударом ладони сжимается, объем газа в нем становится меньше, количество молекул не увеличивается, но так как молекулы расположены плотнее, на единицу площади стенок их количество растет, что приводит к росту давления. Давление разрывает бумагу, резко вырвавшийся воздух является причиной звука в виде хлопка. Получается, давление газа связано и с объемом: давление становится больше с уменьшением объема газа, а если объем газа увеличивается, то давление его уменьшается.
И следующее. У разных газов молекулы различны по массе. С ростом молекулярной массы увеличивается ударная сила молекулы о поверхность, что приводит к росту давления. Поэтому различные газы в одном объеме, с одной и той же температурой оказывают неодинаковые давления.
Итак:
- давление газа определяется общими ударами большого числа молекул о поверхности, окружающие газ;
- если изменить количество молекул газа, его температуру или объем сосуда, в котором газ находится, то можно изменить давление этого газа;
- в одинаковых прочих условиях (число молекул, объем, температура) у различных газов давление неодинаково.
Закон Паскаля
Твердые тела, соприкасаясь с поверхностью, давят на нее перпендикулярно. Газы давят в различных направлениях. А как давят жидкости?
Молекулы жидкости, перемещаясь, долго не задерживаются на месте. Здесь они подобны молекулам газов. Различие лишь состоит в расстояниях между молекулами. Поэтому в жидкостях, как и газах, есть давление, которое действует в любых направлениях одинаково. Почему в ванной вода из крана течет одной струей, а эта же самая вода из душа течет большим количеством одинаковых струек? Если бы вместо душевого сита был шар с дырками, то вода лилась бы во все стороны, и даже вверх. Объясняет эти явления знаменитый закон Паскаля:
Источник
Закон Паскаля справедлив для газов тоже. Примером из жизни служит уже рассмотренное надувание воздушного шарика. Струю воздуха человек направляет прямо перед собой (он же не крутит головой, чтобы заполнить шар), а шар заполняется везде, во всех направлениях. Накачивая резиновую лодку ручным насосом, рыбак нажимает сверху вниз на насос, воздух же наполняет полностью всю форму лодки.
Этот закон давления нашел широчайшее применение в механизмах, использующих принцип работы гидравлического пресса (изобретен Б. Паскалем). Если нажать на маленький поршень S1 силой F1, давление получится p1 = F1/ S1. Это давление без изменения (по закону Паскаля) будет передаваться во всех направлениях и дойдет до поршня S2. Значит, там давление p2 = F2/S2 такое же. p1 = p2, то есть F1/ S1 = F2/S2.
Используя математику, из этого равенства можно получить следующее: F1/F2 = S1/S2. Это равенство выражает закон гидравлического пресса (гидравлический — водяной или жидкостный). Оно означает: действуя маленькой силой на небольшую площадь можно получить большую силу, действующую на большую площадь. Силы будут отличаться во столько же раз, во сколько отличаются площади. Если действовать на малую площадь маленькой силой, используя площадь в несколько раз большую, можно получить силу во столько же раз большую.
Источник
Само слово «пресс» обозначает: механизм для обработки материалов давлением.
С помощью пресса макулатуре, металлолому, сену придают формы удобные для транспортировки.
Методом прессования изготовляют детали сложнейших приборов и машин.
В водяных насосах, отбойных молотках, также используется закон Паскаля и закон гидравлического пресса. Нажимая на тормоз, шофер останавливает автомобиль. Усиленное давление по этим законам передается на тормозные колодки, которые не дают вращаться колесам. Но это, конечно, далеко не весь перечень примеров проявления и использования свойств давления.
Давление жидкости
Можно ли численно рассчитать давление жидкости? Ответ получается, если применить нетрудные математические преобразования.
По определению p = F/S. F – сила, с которой жидкость (ведь она обладает весом P) давит на дно. Дальше, вспомнив формулы веса (P = mg), массы (m = ρV), объема (V = Sh), можно получить:
p = P/S = mg/S = ρVg/S = ρShg/S. Сократить полученную дробь на S, и результат готов:
p = ρgh
Изначально в формуле была задействована площадь дна, а в результате получилось выражение, в котором давление жидкости зависит ни от формы сосуда, ни от площади его стенок и дна, а от плотности ρ и глубины h жидкости (физики называют глубину высотой столба жидкости). Число g ≈ 10 Н/кг осталось от формулы веса.

А теперь самое интересное. Можно ли водой из кружки разрушить большую бочку? Тот факт, что высота столба определяет давление жидкости, позволяет ответить на этот вопрос: « Да, можно!»
Если взять несколько сосудов различной формы, одинаковой высоты и с одинаковой площадью дна, которое затянуто эластичной пленкой, наполнить сосуды водой, то дно прогнется одинаково во всех трех случаях. Хотя вес жидкости разный, сила давления возникает одинаковая (но ведь силой давления является вес!). Что происходит? А вот что:
F = p ∙ S, а p = ρgh и F = ρgh ∙ S
Одна жидкость, плотность ρ, высота h и площадь S дна — одинаковы. Значит, и сила давления одинаковая. Это явление «гидростатического парадокса».
Источник
Первое объяснение этому парадоксу (противоречие с общепринятым утверждением; перевод с греческого «докса» — «мнение», «пара» — «против») дано опять же Б.Паскалем.

Явления, связанные со стоячей жидкостью (в сосуде, в луже, в пруду) и давлением называют гидростатическими.
Сообщающиеся сосуды
Красивое зрелище – действующие фонтаны. Они всегда привлекают к себе внимание детей и взрослых. А каков же их принцип действия?
Первый человек, который это объяснил, опять был Блез Паскаль. Если взять две стеклянные трубочки и соединить их трубкой резиновой, и через воронку наливать воду в одну трубочку, то при любом положении трубочек вода в них будет на одинаковом уровне.
Эти трубочки, а на их месте могут быть любые сосуды, соединяются (сообщаются) друг с другом. Давление в обеих трубочках одинаково (по закону Паскаля), значит, и высота столбиков жидкости в этих соединенных, сообщающихся сосудах — одинакова.
Источник
Если один сосудов поднять на большую высоту, то из второго сосуда жидкость будет стремиться подняться до уровня первого сосуда, но сила тяжести, возвращает ее обратно на землю. Таков основной принцип работы фонтана. Вот его примерная схема:
Фонтан соединяется с большой башней, в которую закачивается вода с помощью насосов. Такую башню называют водонапорной. А если водонапорную башню соединить с водопроводной сетью, то вода поступит в любую квартиру, в любое здание. Водопровод — это пример применения в жизни сообщающихся сосудов.
Источник
К сообщающимся сосудам относятся насосы со шлангами, лейки, чайники, кофейники. В них по два сосуда: емкость под жидкость и носик. Звучит непривычно, но это так.
При помощи сообщающихся сосудов измеряют небольшое давление. Прибор называется жидкостным манометром. Один сосуд закрыт, а ко второму эластичной трубкой присоединена пластмассовая коробочка, затянутая пленкой. Если на пленку нажать, по закону Паскаля давление передастся на жидкость. В одном колене такого манометра жидкость опускается, а в другом поднимается. Давление тем больше, чем больше разница уровней жидкости.

Принцип сообщающихся сосудов используется в шлюзах – устройствах, пропускающих речные корабли через плотины, перегораживающие реки. Плотины обычно устраивают там, где работают гидроэлектростанции. Плотины разделяют течение реки на части: верхнее течение (там накапливается вода) и нижнее. Там, где проходят корабли, сделаны специальные огромные ворота, которые удерживают воду. Получается, что большие сообщающиеся сосуды между собой перекрыты.
Пусть корабль идет по течению реки вниз. Он попадает в верхнюю часть шлюза, где уровень воды высокий. Ворота открываются, и вода начинает перетекать в нижнюю часть, уровень воды снижается, а вместе с ним опускается и корабль (в нижней части наоборот уровень повышается). Снижение происходит до тех пор, пока не произойдет выравнивание (закон сообщающихся сосудов) верхнего и нижнего течений. Корабль может дальше двигаться по реке. Если корабль движется вверх по течению, он вначале попадает в нижнюю часть шлюза. Ворота открываются, вода из верхней части поступает в нижнюю до выравнивания уровней. В нижней части вода поднимается, и вместе с ней поднимается корабль. После выравнивания уровней корабль может двигаться дальше. Шлюзы очень больших плотин могут иметь не одни ворота, а сразу несколько. Ворота могут открываться, как обычные двери (по течению реки) или вертикально.
Источник
Если дно непрозрачного бака соединить с тонкой стеклянной трубкой снизу, расположенной вертикально ему, то можно увидеть высоту воды в баке (см. рисунок). Так устроены водомерные стекла в паровых котлах.
Важный момент. В данных примерах используется одна жидкость. А если в разные сосуды налить разные жидкости, например, воду и керосин. Что будет наблюдаться?
Давление в обоих сосудах одинаково (закон Паскаля). Но ведь плотность воды 1000 кг/м3, а керосина – 800 кг/м3, тогда столб керосина с меньшей плотностью должен быть выше, чем столб воды в 1,25 раза, т. к. плотности отличаются тоже в 1,25 раза.
Наблюдается обратно пропорциональная зависимость:
h1/h2 = ρ2/ρ1

Значит, в сообщающихся сосудах уровни одинаковы для однородной жидкости, а для разных жидкостей уровни различны.