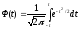Как меняется величина средней ошибки репрезентативности при увеличении дисперсии признака

Любое выборочное
наблюдение ставит своей задачей
определение среднего размера признака
или доли единиц, обладающих данным
признаком, и распространение полученных
характеристик выборочной совокупности
на генеральную совокупность.

Ошибки
репрезентативности
возникают вследствие различия структуры
выборочной и генеральной совокупности.

Структура генеральной
совокупности вполне однозначна, и ей
соответствует вполне определенное
значение среднего размера (или доли)
изучаемого признака. Выборочная же
совокупность формируется на основе
случайного отбора, в силу этого ее состав
отличается от состава генеральной
совокупности, отличается, естественно,
и значение среднего размера (или доли)
изучаемого признака.

Если из одной и той
же генеральной совокупности производится
несколько выборок, то в каждую из них
попадут разные единицы и, следовательно,
каждой выборочной совокупности будет
соответствовать своя средняя. Отсюда
следует важный вывод: выборочная
средняя, в отличие от генеральной, –
величина переменная. Переменной или
случайной величиной будет и ошибка
репрезентативности.

В практических
статистических работах выборочное
наблюдение проводится один раз, поэтому
фактически приходится иметь дело с
одной из множества выборочных средних,
но с какой именно – сказать невозможно.
Чтобы получить суждение о точности
результатов выборочного наблюдения,
математическая статистика дает формулу
средней ошибки,
т.е. средней величины из всех возможных
ошибок при бесчисленном множестве
случайных выборок.

При бесконечно
большом числе выборок получится кривая
частот, которая представляет кривую
выборочного распределения.

Рассмотрим
выборочное распределение средней
величины.
Такое распределение будет являться
нормальным или приближаться к нему по
мере увеличения объема выборки независимо
от того, имеет или не имеет нормальное
распределение та генеральная совокупность,
из которой взяты выборки. С увеличением
числа выборок средняя для всех выборок
будет приближаться к генеральной
средней. По выборочному распределению
может быть рассчитана средняя
квадратическая ошибка репрезентативности:

,

— квадрат ошибки
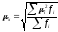
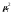
репрезентативности для i-й
выборки,

— число выборок с
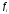
одинаковым значением выборочной средней.

Среднее квадратическое
отклонение выборочных средних от
генеральной средней называется средней
ошибкой выборочной средней (средней
ошибкой выборки для средней величины
признака):

/

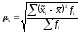
Поскольку, как
правило, генеральная средняя неизвестна,
этой формулой нельзя воспользоваться.
Кроме того, в социально-экономических
исследованиях выборки из одной и той
же совокупности не производятся
многократно. Поэтому используют
нижеприведенную формулу, исходя из
того, что средняя ошибка выборки зависит
от колеблемости признака в генеральной
совокупности и числа отобранных единиц.

Средняя ошибка
выборки для средней величины признака
определяется по формуле:

,

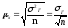
где
²_г
– дисперсия количественного признака
в генеральной совокупности.

Следовательно,
средняя ошибка выборки тем больше, чем
больше вариация в генеральной совокупности,
и тем меньше, чем больше объем выборки.

Т.о. можно утверждать,
что отклонение выборочной средней
от генеральной среднейв среднем равно.
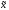
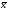
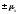
Ошибка конкретной выборки может принимать
различные значения, но ее отношение к
средней ошибке практически не превышает,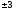
если величина объема выборки достаточно
большая.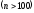

Отношение ошибки
конкретной выборки к средней квадратической
ошибке называется нормированным
отклонением
:.

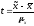
Распределение
нормированного отклонения выборочной
средней от генеральной средней при
численности выборки
определяется следующим уравнением:(1)

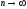
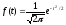
Данное уравнение
называют стандартным
уравнением нормальной кривой.
Величина
достигает максимума при,
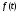
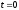
в этом случае.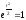

На рис. приведен
график кривой распределения нормированных
отклонений ошибок выборочных средних

.

Рис.

Ординаты соответствуют
плотностям вероятности при том или ином
значении
.
Для того, чтобы определить вероятность
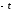
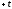
значений в интервале отдо,
следует найти отношение части площади
кривой, заключенной между ординатами,
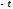
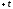
соответствующимиико всей площади кривой. Вся площадь под
кривой нормального распределения
вероятностей принимается за единицу.

Площадь нормальной
кривой, заключенную между ординатами
и,
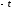
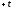
определяют, интегрируя функцию (1) –интеграл
Лапласа.

Имеются таблицы
интеграла Лапласа, которые содержат
значения вероятностей для нормированных
отклонений
.
Значения функции Ф(t) табулированы при
разных значениях, например:

при t=1 P()
= Ф(1) = 0,683;

при t=2 P(2)
= Ф(2) = 0,9545;

при t=3 P(3)
= Ф(3) = 0,9973 и т.д.

Это вероятность
того, что ошибка попадет в заданные
пределы.

В общем виде
=t

характеризует
предельную
ошибку
выборки, показывающую максимально
возможное расхождение выборочной и
генеральной характеристик при
заданной вероятности
этого утверждения. Т.о. о величине ошибки
можно судить с определенной вероятностью.

Так, при t=2 возможная
ошибка 
не превысит 2,
что гарантируется с вероятностью 0,9545.
Это значит, что в 9545 выборках из 10000
подобных максимальная ошибка не выйдет
за пределы 2

где
– это коэффициент доверия.

При проведении
выборочного учета массовых
социально-экономических явлений
считается достаточным максимальный
размах ошибки выборки 3.

На практике наиболее
часто пользуются значениями вероятности
Р=0,95 (t=1,96), Р=0,99 (t=2,58) и Р=0,999 (t=3,28),
гарантирующими репрезентативность
выборки соответственно с ошибкой 5; 1;
0,1%.

Предельная ошибка
выборки позволяет определять предельные
значения характеристик генеральной
совокупности при заданной вероятности,
т.е. их доверительные
интервалы.

Поэтому вероятность
Р называется доверительной,
она представляет собой вероятность
того, что ошибка выборки не превысит
некоторую заданную величину ,
т.е. генеральная
средняя
находится где-то в пределах

(от
до),

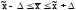
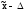
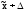
генеральная доля
– в пределах
(от w–
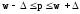
до w+).

Как мы определили
выше, средняя
ошибка выборки для средней величины
признака
определяется по формуле:
,

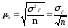
где
²_г
– дисперсия количественного признака
в генеральной совокупности.

Если при выборочном
наблюдении изучению подлежит альтернативный
признак, то средняя
ошибка выборки для доли единиц,
обладающих данным признаком, определяется
по теореме Я. Бернулли:

,

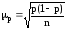
где
p – доля единиц, обладающих данным
качеством, в генеральной совокупности;
p(1-p) – дисперсия альтернативного признака
в генеральной совокупности.

Приведенные формулы
средних ошибок выборки практически
непригодны для расчета. В них фигурирует
дисперсия признака в генеральной
совокупности, которая неизвестна, как
неизвестна и генеральная доля, генеральная
средняя. Поскольку в теории вероятности
доказано, что
,

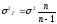
то при большом
объеме выборки дисперсии генеральной
²_г
и выборочной ²
совокупностей равны. ().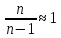
Это дает основание исчислять среднюю
ошибку выборки по значениям выборочной
дисперсии²
для средней и w(1–w) для доли признака:

,,

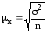
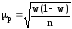
где
w – доля признака в выборочной совокупности.

Наряду с абсолютной
величиной предельной ошибки выборки
рассчитывается и относительная
ошибка
выборки, которая определяется отношением
предельной ошибки средней или доли к
соответствующей характеристике
выборочной совокупности:
;.

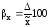
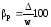
При проведении
выборочного наблюдения в экономических
исследованиях преимущественно стремятся
к тому, чтобы относительная ошибка
репрезентативности выборки не превышала
5 … 10%.

Вывод формул

,,

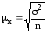
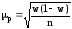
исходит из схемы
повторной
выборки. На
практике повторная выборка, при которой
численность генеральной совокупности
остается неизменной (т.е.отобранная
единица возвращается в генеральную
совокупность и снова может быть отобрана),
встречается редко (например, при изучении
населения в качестве пользователей,
пациентов, избирателей).

Обычно отбор
организуется по схеме бесповторной
выборки, при которой отобранная единица
после обследования в генеральную
совокупность не возвращается и в
дальнейшей выборке не участвует.

При бесповторной
выборке численность генеральной
совокупности в процессе отбора сокращается
на

1–n/N, где n/N –
доля отобранных единиц.

В связи с этим
формулы ошибки выборки приобретают
следующий вид:

;

.

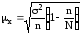
Так как доля единиц
генеральной совокупности, не попавших
в выборку (1–n/N), всегда меньше единицы,
то ошибка выборки при бесповторном
отборе при прочих равных условиях
меньше, чем при повторном отборе.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

First, I’d like to blow your mind: Increasing sample size does not decrease the variance of an estimate. What you call variance can, for example, stay essentially flat, even as $n$ goes to infinity. But let’s come back to that.

We need to define terms. What you’re referring to as «variance» is generally called standard error, the standard deviation of the sampling distribution of the statistic. A statistic’s sampling distribution is just the distribution of all possible values the estimate could take, over all possible samples of a given size drawn from the population of interest. So, when you ask why variance decreases with sample size, you’re really asking why the sampling distribution of a statistic is wider for smaller $n$ and narrower for larger $n$. For the vast majority of practical statistics, your assumption that this will be the case is correct.

The reason this tends to be the case is, as others have said, the Central Limit Theorem. However, what others have neglected to tell you is that there are many limit theorems. Which one applies depends on a) the family of distributions a statistic’s sampling distribution belongs to, and b) the asymptotic behavior of the distribution as $n$ goes to infinity.

The vast majority of statistics have a sampling distribution that is approximately and asymptotically normal, so the famous Central Limit Theorem applies. Normal distributions get skinnier as n increases, for reasons others detail. Having a normal sampling distribution gives a statistic a property called efficiency, which just means its observed value gets closer to its expected value with increasing $n$.

That’s exactly what we want. We therefore purposely choose statistics with this property when we have the option. It’s easy to assume that all statistics have this property when all statistics you see have it, but I guess that’s what you’d call selection bias. (It’s also called stats being oversimplified for beginners because it’s hard enough as it is!)

A particularly interesting counterexample is a certain function of the Hamming distance, computed between a pair of bivariate normal random vectors that have been converted to ranks without ties. That is, suppose you draw $n$ pairs at random from a bivariate normal population with correlation parameter $rho$, $(X, Y)$. You replace each real number in $X$ with an integer indicating its relative order in $X$ after sorting the vector (first $= 1$, second $= 2$, and so on), and the same for $Y$.

You then count the number of bivariate observations with equal ranks. (So, the count equals $n$ minus the Hamming distance between $X$ and $Y$.) This count’s sampling distribution is approximately and asymptotically Poisson with parameter $np$, where $p$ is the probability of obtaining at least one pair of equal ranks (Zolotukhina and Latyshev, 1987).

It is well known that $np = 1$ when $rho = 0$ (As first shown by Montmort in 1708). Because a Poisson variable’s parameter is equal to both its mean and its variance, the standard error of the count only gets closer and closer to $1$ as sample size increases, when $rho = 0$ (Rae, 1987; Rae and Spencer, 1991). Cool, right? In general, for $rho geq 0$, the variance converges to $1/(1 — rho)$ as $n$ goes to infinity (Zolotukhina and Latyshev, 1987) under bivariate normality. It does NOT decrease for non-negative $rho$.