Define absolute error

Let’s first know some basics about numbers used  in floating-point arithmetic or in other words Numerical analysis and how they are calculated.

Basically, all the numbers that we use in Numerical Analysis are of two types as follows.

• Exact Numbers –
  Numbers that have their exact quantity, means their value isn’t going to change. For example- 3, 2, 5, 7, 1/3, 4/5, or √2 etc.
• Approximate Numbers –
  These numbers are represented in decimal numbers. They have some certain degrees of accuracy. Like the value of π is 3.1416 if we want more precise value, we can write 3.14159265, but we can’t write the exact value of π.

  These digits that we use in any approximate value, or in other way digits which represent the numbers are called Significant Digits.

How to count significant digits in a given number :
For example –
In the normal value of π (3.1416), there are 5 significant digits and when we write more precise value of it (3.14159265) we get 9 significant digits.
Let’s say we have numbers: 0.0123, 1.2300, and 0.10234. Now we have 4, 3, and 5 significant digits respectively.
In the Scientific Representation of numbers –
2.345×10⁷, 8.7456 ×10⁴, 5.4×10⁶ have 4, 5 and 2 significant digits respectively.

Absolute Error :
Let the true value of a quantity be X and the approximate value of that quantity be X₁. Hence absolute error has defined the difference between X and X₁. Absolute Error is denoted by E_A.

Hence EA= X-X1=δX 

Relative Error :
It is defined as follow.

ER = EA/X = (Absolute Error)/X

Percentage Error :
It is defined as follow.

EP= 100×EP= 100×EA/X

Let’s say we have a number δX = |X₁-X|_,   It is an upper limit on the magnitude of Absolute Error and known as Absolute Accuracy.

Similarly the quantity δX/ |X| or δX/ |X₁| called Relative Accuracy.

Now let’s solve some examples as follows.

• Ex-1 :
  We are given an approximate value of π is 22/7 = 3.1428571 and true value is 3.1415926. Calculate absolute, relative and percentage errors?
  Solution –

  We have True value X= 3.1415926, And Approx. value X1= 3.1428571.
  So now we calculate Absolute error,  we know that  EA= X - X1=δX
  Hence EA= 3.1415926- 3.1428571 = -0.0012645
  
  Answer is -0.0012645
  Now for Relative error we’ve (absolute error)/(true value of quantity) 
  Hence ER =  EA/X = (Absolute Error)/X, EA=(-0.0012645)/3.1415926  = -0.000402ans.
  
  Percentage Error, 
  EP= 100 × EA/X = 100 × (-0.000402) = - 0.0402ans.

• Ex-2 :
  Let the approximate values of a number 1/3 be 0.30, 0.33, 0.34. Find out the best approximation.
  Solution –
  Our approach is that we first find the value of Absolute Error, and any value having the least absolute will be best. So, we first calculate the absolute errors in all approx values are given.
  <pre
  |X-X₁| = |1/3 – 0.30| = 1/30
  |1/3 – 0.33| = 1/300
  |1/3 – 0.34| = 0.02/3 = 1/500

  Hence, we can say that 0.33 is the most precise value of 1/3;
• Ex-3 :

  Finding the difference—

  √5.35 - √4.35
  

  Solution –

   
  √5.35 = 2.31300
  √4.35 = 2.08566
  Hence, √5.35 - √4.35 = 2.31300 – 2.08566 = 0.22734
  

  Here our answer has 5 significant digits we can modify them as per our requirements.

Measurement is a major part of scientific calculations. Completely accurate measurement results are absolutely rare. While measuring different parameters, slight errors are common. There are different types of errors, which cause differences in measurement. All the errors can be expressed in mathematical equations. By knowing the errors, we can calculate correctly and find out ways to correct the errors. There are mainly two types of errors – absolute and relative error. In this article, we are going to define absolute error and relative error. Here, we are giving explanations, formulas, and examples of absolute error and relative error along with the definition. The concept of error calculation is essential in measurement. 

Define Absolute Error

Absolute error is defined as the difference between the actual value and the measured value of a quantity. The importance of absolute error depends on the quantity that we are measuring. If the quantity is large such as road distance, a small error in centimetres is negligible. While measuring the length of a machine part an error in centimetre is considerable. Though the errors in both cases are in centimetres, the error in the second case is more important.

Absolute Error Formula

The absolute error is calculated by the subtraction of the actual value and the measured value of a quantity. If the actual value is x₀ and the measured value is x, the absolute error is expressed as,

∆x = x₀- x

Here, ∆x is the absolute error.

Absolute Error Example

Here, we are giving an example of the absolute error in real life. Suppose, we are measuring the length of an eraser. The actual length is 35 mm and the measured length is 34.13 mm. 

So, The Absolute Error = Actual Length — Measured Length

 = (35 — 34.13) mm 

 = 0.87 mm

Classification Of Absolute Error

1. Absolute accuracy error

Absolute accuracy error is the other name of absolute error. The formula for absolute accuracy error is written as E= E exp – E true, where E is the absolute accuracy error, E exp is the experimental value and E true is the actual value.

1. Mean absolute error

MAE or the mean absolute error is the mean or average of all absolute errors. The formula for Mean Absolute Error is given as,

MAE = [frac{1}{n}] [sum_{i=1}^{n}mid x_{i} -xmid]

1. Absolute Precision Error

It is a standard deviation of a group of numbers. Standard deviation helps to know how much data is spread.

Relative Error Definition

The ratio of absolute error of the measurement and the actual value is called relative error. By calculating the relative error, we can have an idea of how good the measurement is compared to the actual size. From the relative error, we can determine the magnitude of absolute error. If the actual value is not available, the relative error can be calculated in terms of the measured value of the quantity. The relative error is dimensionless and it has no unit. It is written in percentage by multiplying it by 100.

Relative Error Formula

The relative error is calculated by the ratio of absolute error and the actual value of the quantity. If the absolute error of the measurement is ∆x, the actual value is x0, the measured value is x, the relative error is expressed as, 

                                                     xᵣ = (x₀ — x)/ x₀ = ∆x/x₀

Here, xr is the relative error.

Relative Error Example

Here, we are giving an example of relative error in real life. Suppose, the actual length of an eraser is 35 mm. Now, the absolute error = (35-34.13) mm = 0.87 mm.

So, the relative error = absolute error/actual length

= 0.87/35

= 0.02485

(Image will be Uploaded Soon)

Relative Error as a Measure of Accuracy

In many cases, relative error is a measure of precision. At the same time, it can also be used as a measure of accuracy. Accuracy is the extent of knowing how accurate the value is as compared to the actual or true value. Students can find the RE accuracy only if they know the true value or measurement. For simplicity, we have the formula for calculating the RE accuracy which is given as

RE[_{accuracy}] = Actual error/ true value * 100%

Absolute Error and Relative Error in Numerical Analysis

Numerical analysis of error calculation is a vital part of the measurement. This analysis finds the actual value and the error quantity. The absolute error determines how good or bad the measurement is. In numerical calculation, the errors are caused by round-off error or truncation error.

Absolute and Relative Error Calculation — Examples

1. Find the absolute and relative errors. The actual value is 125.68 mm and the measured value is 119.66 mm.

Solution:

Absolute Error = |125.68 – 119.66| mm

= 6.02 mm

Relative Error = |125.68 – 119.66| / 125.68

= 0.0478

2. Find out the absolute and relative errors, where the actual and measured values are 252.14 mm and 249.02 mm.

Solution:

Absolute Error = |252.14 – 249.02| mm

                           = 3.12 mm

Relatives Error = 3.12/252.14

= 0.0123

Did You Know?

In different measurements, the quantity is measured more than one time to get an average value of the quantity. Mean absolute error is one of the most important terms in this kind of measurement. The average of all the absolute errors of the collected data is called the MAE ( Mean Absolute Error). It is calculated by dividing the sum of absolute errors by the number of errors. The formula of MAE is –

MAE = [frac{displaystylesumlimits_{i=1}^n mid x_{0}-x mid }{n}]

Here, 

n is the number of errors, 

x₀ is the actual value, 

x is the measured value, and 

|x₀-x| is the absolute error.

From Wikipedia, the free encyclopedia

In statistics, mean absolute error (MAE) is a measure of errors between paired observations expressing the same phenomenon. Examples of Y versus X include comparisons of predicted versus observed, subsequent time versus initial time, and one technique of measurement versus an alternative technique of measurement. MAE is calculated as the sum of absolute errors divided by the sample size:^[1]

It is thus an arithmetic average of the absolute errors , where is the prediction and the true value. Note that alternative formulations may include relative frequencies as weight factors. The mean absolute error uses the same scale as the data being measured. This is known as a scale-dependent accuracy measure and therefore cannot be used to make comparisons between series using different scales.^[2] The mean absolute error is a common measure of forecast error in time series analysis,^[3] sometimes used in confusion with the more standard definition of mean absolute deviation. The same confusion exists more generally.

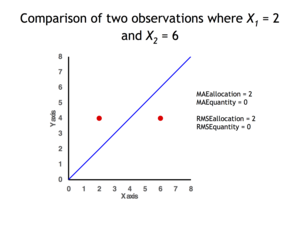
Quantity disagreement and allocation disagreement[edit]

It is possible to express MAE as the sum of two components: Quantity Disagreement and Allocation Disagreement. Quantity Disagreement is the absolute value of the Mean Error given by:^[4]

Allocation Disagreement is MAE minus Quantity Disagreement.

It is also possible to identify the types of difference by looking at an plot. Quantity difference exists when the average of the X values does not equal the average of the Y values. Allocation difference exists if and only if points reside on both sides of the identity line.^[4][5]

[edit]

The mean absolute error is one of a number of ways of comparing forecasts with their eventual outcomes. Well-established alternatives are the mean absolute scaled error (MASE) and the mean squared error. These all summarize performance in ways that disregard the direction of over- or under- prediction; a measure that does place emphasis on this is the mean signed difference.

Where a prediction model is to be fitted using a selected performance measure, in the sense that the least squares approach is related to the mean squared error, the equivalent for mean absolute error is least absolute deviations.

MAE is not identical to root-mean square error (RMSE), although some researchers report and interpret it that way. MAE is conceptually simpler and also easier to interpret than RMSE: it is simply the average absolute vertical or horizontal distance between each point in a scatter plot and the Y=X line. In other words, MAE is the average absolute difference between X and Y. Furthermore, each error contributes to MAE in proportion to the absolute value of the error. This is in contrast to RMSE which involves squaring the differences, so that a few large differences will increase the RMSE to a greater degree than the MAE.^[4] See the example above for an illustration of these differences.

Optimality property[edit]

The mean absolute error of a real variable c with respect to the random variable X is

Provided that the probability distribution of X is such that the above expectation exists, then m is a median of X if and only if m is a minimizer of the mean absolute error with respect to X.^[6] In particular, m is a sample median if and only if m minimizes the arithmetic mean of the absolute deviations.^[7]

More generally, a median is defined as a minimum of

as discussed at Multivariate median (and specifically at Spatial median).

This optimization-based definition of the median is useful in statistical data-analysis, for example, in k-medians clustering.

Proof of optimality[edit]

Statement: The classifier minimising is .

Proof:

The Loss functions for classification is

Differentiating with respect to a gives

This means

Hence

See also[edit]

• Least absolute deviations
• Mean absolute percentage error
• Mean percentage error
• Symmetric mean absolute percentage error

References[edit]

You’re on the right track. Of course you can’t find the actual error because you don’t know the actual values. Thus you want to constrain the error. First note that we’re talking about rounding error (as you’ve done), thus the maximum that each variable can be off by is 0.5 of its precision, i.e.

|e₁| <= 0.005

|e₂| <= 0.005

|e₃| <= 0.05

For the absolute error of x₁-x₂+x₃, the worst case is that all of the errors add together linearly, I.e.:

|e₁₂₃| <= 0.005+0.005+0.05 = 0.06.

Because it’s absolute error, you don’t have to rescale by what the actual values of x₁… are.

For the relative error of (x₁x₂)/x₃, it’s a little more complicated—you have to actually propogate (multiply) out the error. But, if you assume that the error is much smaller than the value, i.e. |e₁| << x₁ (which is a good approximation for this case), then you get the equation that you used in ‘b’:

|r| = |r₁₂₃ / (x₁x₂/x₃) | ~< |e₁/x₁| + |e₂/x₂| + |e₃/x₃|

Because this is relative error, you do have to rescale the errors by the actual values.

So, overall, you just about had it right — just a little trouble with the absolute error.

Absolute Error Formula
Absolute error is defined as the magnitude of difference between the actual and the individual values of any quantity in question.

Say we measure any given quantity for n number of times and a₁, a₂ , a₃ …..a_n are the individual values then

Arithmetic mean a_m = [a₁+a₂+a₃+ …..a_n]/n

a_m= [Σ_i=1ⁱ⁼ⁿ a_i]/n

Now absolute error formula as per definition =
Δa₁= a_m – a₁
Δa₂= a_m – a₂
………………….
Δa_n= a_m – a_n

Mean Absolute Error= Δa_mean= [Σ_i=1ⁱ⁼ⁿ |Δa_i|]/n
Note: While calculating absolute mean value, we dont consider the +- sign in its value.

Relative Error or fractional error
It is defined as the ration of mean absolute error to the mean value of the measured quantity
δa =mean absolute value/mean value = Δa_mean/a_m

Percentage Error
It is the relative error measured in percentage. So
Percentage Error =mean absolute value/mean value X 100= Δa_mean/a_mX100

An example showing how to calculate all these errors is solved below
The density of a material during a lab test is 1.29, 1.33, 1.34, 1.35, 1.32, 1.36 1.30 and 1.33

So we have 8 different values here so n=8

Mean value of density u= [1.29+1.33+1.34+1.35+1.32+1.36+1.30+1.33] / 8 = 1.3275 = 1.33 (rounded off)

Now we have to calculate absolute error for each of these 8 values
Δu₁ = 1.33 – 1.29 = 0.04
Δu₂ = 1.33 – 1.33= 0.00
Δu₃ = 1.33 – 1.34= -0.01
Δu₄ = 1.33 – 1.35= -0.02
Δu₅ = 1.33 – 1.32= 0.01
Δu₆ = 1.33 – 1.36= -0.03
Δu₇ = 1.33 – 1.30= 0.3
Δu₈ = 1.33 – 1.33= 0.00

Now remember we don’t take +- signs in calculating Mean absolute value
So mean absolute value = [0.04+0.00+0.01+0.02+0.01+0.03+0.03+0.00]/8 = 0.0175 = 0.02 (rounded off)

Relative error = +- 0.02/1.33 =+- 0.015 = +- 0.02

Percentage error = +- 0.015*100 = +- 1.5%